中小企業診断士のたかぴーです。
今回はスルツキー分解について解説していこうと思います。
効用理論は、このあたりからだんだんと内容が難しくなっていきますので、経済学が嫌になってくる方も多いのではないでしょうか?
できるだけ数学が苦手な方にも分かるように分かりやすく解説したいと思いますので、是非最後までご覧ください。
↓YouTube動画でも解説中!
予算制約線と無差別曲線の関係
まずは前回までの復習です。
予算制約線と無差別曲線の関係について確認しましょう。
予算制約線とは、予算をすべて使った場合に購入できる2財の消費量の組み合わせを表した直線のことを言うのでしたね。
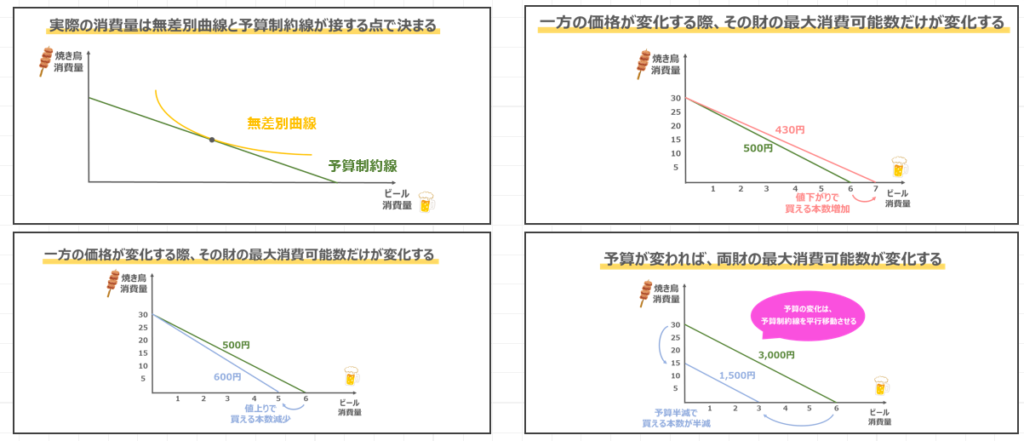
そして、予算制約線と無差別曲線の接点で、実際の消費量は決定するのでした。
予算戦略戦の特徴について掘り下げていくと、一方の財の価格が変化する際、その財の最大可能数だけが変化するのでしたね。
価格が上がれば最大消費可能数は減少して、価格が下がれば最大消費可能数は増加するのでした。
そして、予算そのものが変わったときは、予算制約線が平行移動するのでしたね。
ここまでの内容に少しでも不安があれば、前回までの記事を見直して、よく復習していただければと思います。

スルツキー分解とは?
それではスルツキー分解について確認していきましょう。
スルツキー分解とは、一方の財の価格変化が両材の消費量に与える影響を分析する手法とされています。
例えば、横軸にピールの消費量、縦軸に焼き鳥の消費量をとって、予算制約線と無差別曲線がこのように描けたとしましょう。

この時、ビールの消費量は2杯で、焼き鳥の消費量は10本だったとします。
ここでビールをさらに低価格で販売することで、予算制約線と無差別曲線の接点がこのように変化したことを考えてみます。
ビールの消費量は4杯、焼鳥の消費量が15本になったとします。
グラフから、ビールの価格減少でビールと焼き鳥の消費量が増加していることが読み取れますね。
この両財の消費量の変化を、代替効果と所得効果の2つに分けて考えるのが、スルツキー分解のアプローチとなります。
代替効果とは?
ここからはこの代替効果と所得効果の2つについて詳しく見ていきたいと思います。
まず代替効果とは変化した際の価格比で、変化前と同じ効用を得るための消費の変化量を指します。
例えば焼き鳥とビールの消費について考えるときに、予算制約線と無差別曲線が下図に描けていたとしましょう。グレーの点線と曲線がもともとの予算制約線と無差別曲線を表します。

そしてビールの価格が減少して、予算制約線が赤線のように変化したとします。
このとき、消費量は点Aから点Bに変化しています。
ここで、代替効果では価格変化した時と同じ価格比を考えます。
具体的な数字を当てはめた方が考えやすいので、画像右の表で考えましょう。
価格変化前は予算が2000円、ビールが一杯500円、焼き鳥が一本100円だったとします。
価格変化後は予算と焼き鳥の価格は変わらず、ビールだけが一杯125円にまで値下がりしたと考えます。
このビール一杯125円と焼鳥一本100円という価格比で、元々の予算制約線と同じ効用を得られる消費量を考えるわけですね。
前回の記事で、価格比は予算制約線の傾きで表されると説明をしました。
代替効果を考えるときは、新しい予算成約線と平行な直線を、元々の無差別曲線と接するように描きます。画像での青色の直線ですね。
こうすることで、価格変化後の価格比で、価格変化前と同じ効用を得られる消費量を考えられるわけですね。
接点の数値を読み取ると、ビールの消費量は2杯から3杯に増え、焼き鳥の消費量は10本から5本に減っていることが読み取れます。
この変化を代替効果と呼ぶわけですね。
代替効果では、もともとの価格比と比較して、相対的に安くなったビールの消費量を増やし、逆に相対的に高くなった焼き鳥の消費量を減らしているということが読み取れます。
この価格変化後の予算制約線把握した上で、それと平行な直線を引いて分析するという点がポイントです。
最初は難しく感じるかもしれませんが、付いてこれなかった方は、繰り返し確認してみてください。
所得効果とは?
続いて所得効果です。
所得効果は価格が変化した際の、実質所得の変化による消費量の変化量を見ていきます。
先ほどまでの説明では、点Aから点Cへの移動は代替効果と言いました。

表で確認してみると、価格変化前と価格変化後の予算とビール1杯、焼き鳥1本のそれぞれの価格は画像右側のように表されました。
そして青色の直線で表した補助線について見てみると、ビールと焼き鳥の価格比は価格変化後と同じですので、ビール一杯125円で焼鳥一本100円であることがわかりますね。
そしてこの時の予算は、計算してみると875円であることがわかります。
この875円と、もともとの予算2,000円の差が実質所得の増加とみなせるわけですね。
グラフに目を移してみますと、青い直線は赤い直線に平行移動したと見なすことができます。
予算制約線が平行移動するのは、予算が増加するときでしたね。
この点Cから点Bへの消費量の変化を所得効果と呼んでいます。
実際に変化量を見てみると、ビールの消費量が3杯から4杯に増加して、焼き鳥の消費量も5本から15本に増加していることが読み取れます。
所得効果では、実質所得の増加で、両財の消費量が増加していることが読み取れます。
以上がスルツキー分解の分析手順の説明でした。
本試験では、グラフを読み取れることが大切ですので、点Aから点Cへの消費量の変化が代替効果、点Cから点Bへの変化が所得効果であるということを改めて確認してください。
過去問を解いてみよう (平成26年度 第16問 改題)
それでは、ここまでの内容を、過去問を解いて復習をしてみましょう。
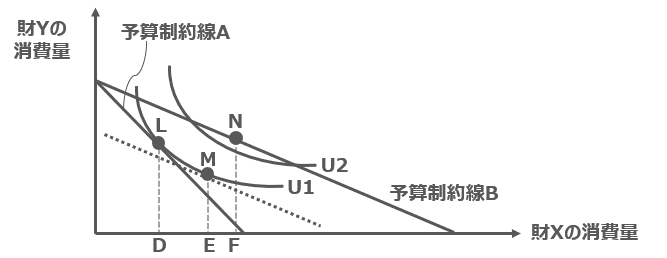
下図は、財Xと財Yを消費する合理的個人が予算制約線Aに直面し、予算制約線Aと無差別曲線U1との接点Lで効用を最大化する状態を描いている。他の条件を一定として、財Xの価格の低下によって予算制約線がBへと変化すると、この合理的個人は、予算制約線Bと無差別曲線U2との接点Nを選択することで効用を最大化することができる。なお、破線で描かれた補助線は、予算制約線Bと同じ傾きを有し、点Mで無差別曲線U1と接している。この図に関する説明として最も適切なものを下記の解答群から選べ。
ア この図における財Xは、下級財の特性を示している。
中小企業診断士試験 経済学 平成26年度 第16問 改題
イ 点Lから点Nへの消費量の変化のうち、「所得効果」は点Lから点Mへの変化によって示されている。
ウ 点Lから点Nへの消費量の変化のうち、「代替効果」は点Mから点Nへの変化によって示されている。
エ 財Xの価格の低下による「代替効果」のみを考えると、財Yの消費量が減少することが示されている。
図から読み取れる内容を答える問題ですね。
選択肢を一つ一つ見ていきましょう。
✅選択肢ア
財Xは下級財の特性を示しているとありますね。
これはこの次の経済学の動画で解説する内容となりますが、実質所得の増加によって、消費量が増える財は、下級財ではなく上級財と言いますので、選択肢アは誤りとなります。
ただし、この選択肢がわからなくてもこの問題は解けますね。
✅選択肢イ
所得効果は点Lから点Mの変化によって示されるとありますね。
点Lから点Mへの移動は、もともとの無差別曲線上の移動です。
このような変化は、代替効果というので、選択肢イは誤りとなります。
✅選択肢ウ
代替効果は点Mから点Nへの変化によって示されるとあります。
今度はもともとの無差別曲線から新しい無差別曲線への変化ですので、これは所得効果を表しています。
ですので、選択肢ウも誤りとなりますね。
✅選択肢エ
代替効果のみを考えると、財Yの消費量が減少していることが示されているとあります。
グラフに青色の矢印で示した代替効果を見てみると、確かに財Yの消費量が減少していることが読み取れますので、選択肢エが正解であることが読み取れますね。
スルツキー分解の問題は、難しく感じるかもしれませんが、一度理解してしまえば簡単であることが多いので、早めに攻略しておきましょう。
まとめ
それでは最後にまとめです。
今回学んだスルツキー分解は、一方の財の変化が、両財の消費量に与える影響を分析する手法なのでした。
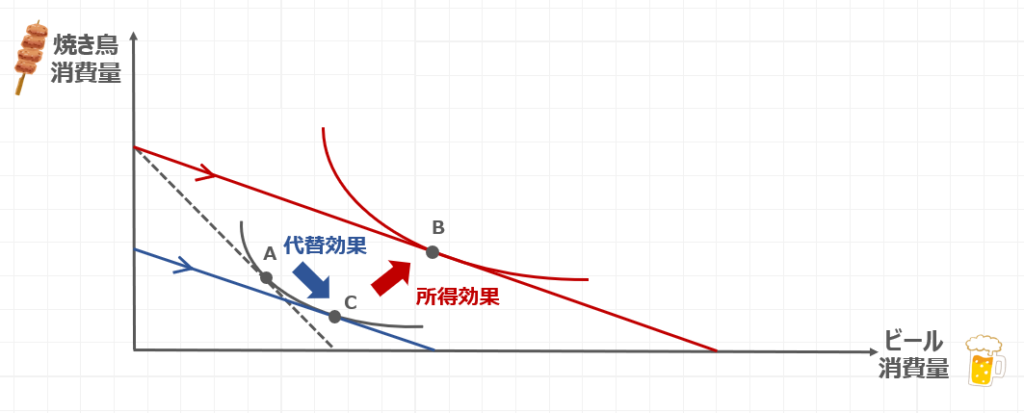
具体的には予算制約線と無差別曲線によって決定していた消費量点Aが、一方の価格の変化量によって、消費量が点Bに移動するときに、この消費量の変化を代替効果と所得効果で分析するのでしたね。
代替効果については、新しい予算制約線と平行で、もともとの無差別曲線と接するような直線を描いたときに、点Aから新しくできた接点である点Cへの消費量の変化を代替効果と呼ぶのでしたね。
続いて所得効果は、点Cから点Bへの消費量の変化として表すことができます。
青の直線から赤の直線への移動を所得の増加とみなして、実質所得の増加による消費量の変化と捉えるわけですね。
というわけで、今回はスルツキー分解について解説をしました。
予算制約線と無差別曲線が2本ずつ出てきて、さらに補助線まで登場するので、かなりグラフが複雑になり、初見で理解するのが難しい論点とはなっています。
ぜひご自身で過去問を解いてみて、少しでも分からなければ記事を見直しながら、学習も進めていただければと思います。
経済学は一度理解してしまえば、そこまで暗記量は少なくて済む科目です。
早めに攻略することで、一次試験本番前の学習を優位に進められますので、これからも一緒に学習を続けていきましょう。
それでは今回の解説記事はここまでとしたいと思います。
ここまでご覧いただき、ありがとうございました。
それではまた次回の解説記事でお会いしましょう。勉強頑張ってください!応援しています。さようなら!!