中小企業診断士のたかぴーです。
今回は効用理論の最後の論点である、ギッフェン財について解説してみたいと思います。
この論点は今まで学習してきた内容の、集大成のような論点なので、ここまで理解できれば効用理論は完璧といえますね。
まだ過去の動画を見てないという方は、過去記事もチェックした後でご覧いただければと思います。
↓YouTube動画でも解説中!
上級財・中級財・下級財とは?
まず、上級財・中級財・下級財は、所得変化による消費量の変化に応じた財の分類です。
具体例を見ながら中身を確認してみましょう。

まず上級財とは、所得が増えたら消費量が増える財のことを言います。
具体例としては、旅行が当てはまりますね。
なかなか家計に余裕がない旅行に行けませんが、一般的に所得に余裕ができたら旅行する頻度は増えると思いますので、このような財が上級財に当てはまるわけですね。
続いて中級財とは、所得が増えても消費量が変わらない財のことを言います。
具体例としては、トイレットペーパーのような必需品が当てはまりますね。
自分の給料が増えたからといって、トイレに行く頻度が増えるわけではありませんし、当然、トイレットペーパーの消費量が変化するものでもありません。
こういったものが中級財に含まれるわけですね。
最後に、下級財は所得が増えたら消費量が減る財のことを言います。
具体例としては、発泡酒が当てはまりますね。
発泡酒は安くておいしいわけですが、やっぱり飲み比べるとビールの方がおいしいですよね。
安いという理由で発泡酒を飲んでいた方も、所得に余裕ができれば積極的にビールを買うようになるのではないでしょうか。
結果的に、ビールの消費量が増えた分、発泡酒の消費量は減ることになるわけです。
このように所得が増えたら消費量が減る財を下級財と言うのですね。
それでは、このそれぞれの財について、グラフの読み解き方を解説していきたいと思います。
スルツキー分解とは?
グラフ読み取りについては、前回解説したスルツキー分解を理解しておく必要がありますので、簡単に内容をおさらいしておきましょう。
スルツキー分解とは、一方の財の価格の変化が、両財の消費量に与える影響を分析する手法なのでした。
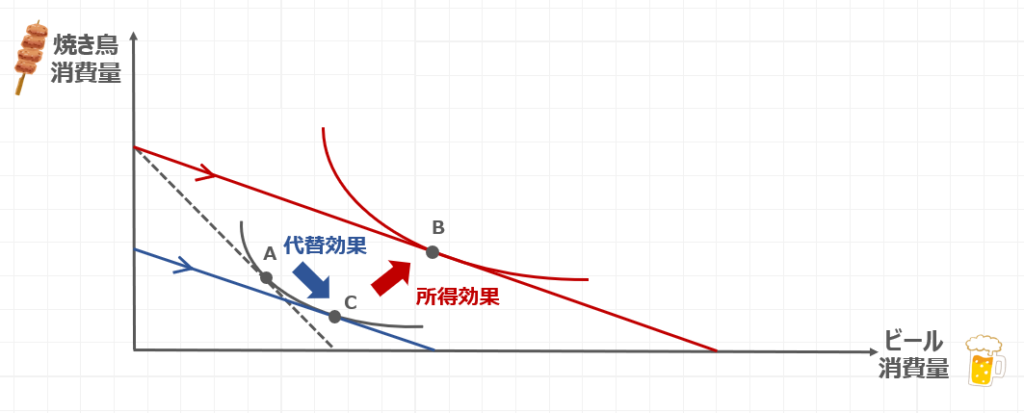
具体的には、ビールと焼き鳥の消費量を考えた際に、上図の点線の予算制約線と無差別曲線が描けたとします。
そして、ビールの価格が下がり、予算制約線がこのような赤い線のように変化したとしましょう。
この点Aから点Bへの消費量の変化をスルツキー分解によって分析するわけですね。
分析する際は、新しい予算制約線と平行で、もともとの無差別曲線と接するような接線を描き、接点を点Cとします。
そして、点Aから点Cへの消費量の変化を代替効果と呼んで、点Cから点Bへの消費量の変化を所得効果と呼ぶのでしたね。
点Cから点Bの消費量の変化は、実質所得が増えたことの影響と捉えますので、所得が増えたことによる消費量の変化を分析することができるようになります。

それでは各財について、どのようにグラフで描けるのか確認してみましょう。
上級財の見分け方
上級財は所得が増えたら消費量が増える財でしたね。
先ほど描いたグラフが、まさに上級財を表しています。
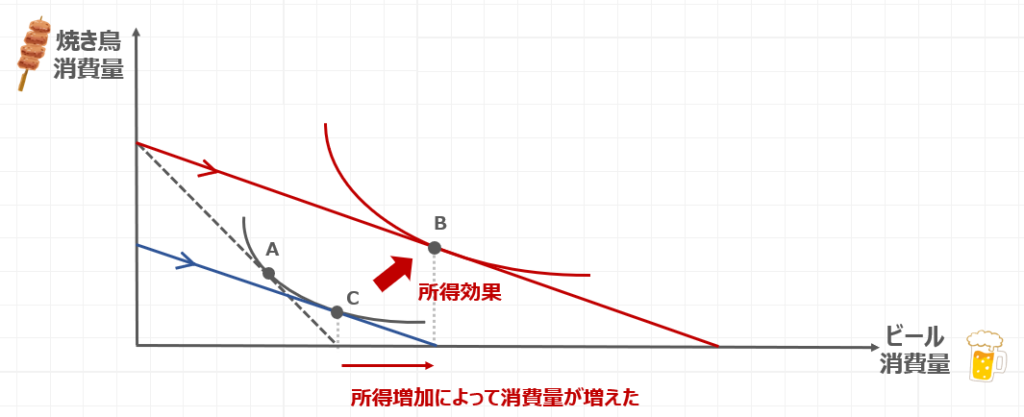
グラフから、ビールの消費量は所得効果によって増えていることが読み取れます。
所得効果は実質所得の増加とみなせるので、所得増加によって消費量が増えたと読み取ることができます。
ですので、このケースでは、ビールは上級財であると読み取ることができるわけですね。
中級財の見分け方
続いて中級財です。
中級財は所得が増えても、消費量が変わらない財のことを言うのでしたね。
グラフで表すと以下のようになります。
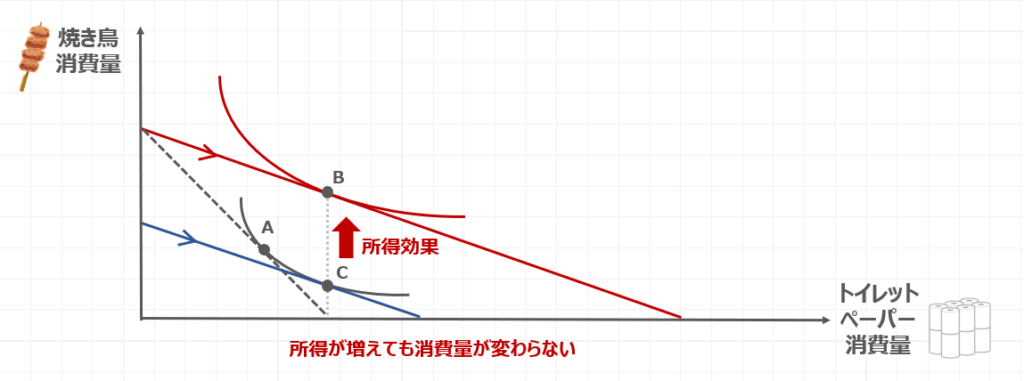
トイレットペーパーが安くなったことによって、予算制約線が外側に平行移動しているので、実質所得が増加していると読み取れます。
一方で、トイレットペーパーの消費量は、点Cと点Bで変わっていません。
これは所得が増えても消費量が変わらないことを表しているので、トイレットペーパーは中級財であると読み取ることができます。
下級財の見分け方
最後に下級財です。
下級財は所得が増えたら消費量が減るのでした。
グラフで表すと、以下のようになりますね。
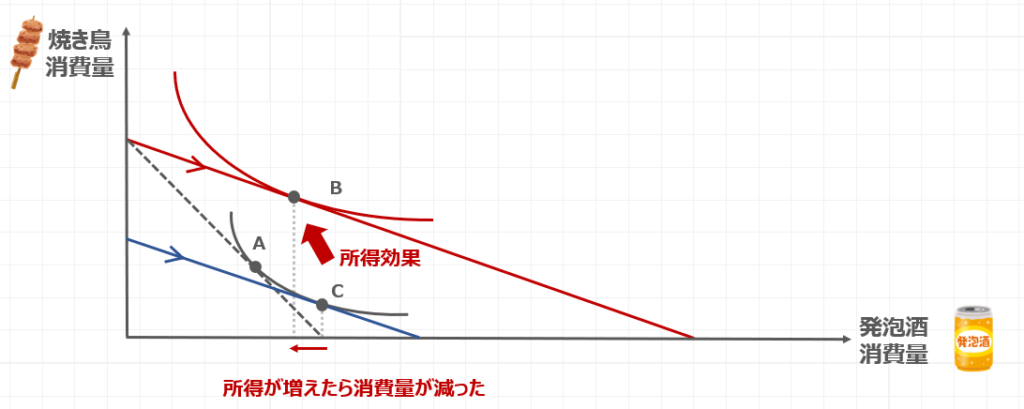
発泡酒の価格が下がったことで実質所得は増えていますが、発泡酒の消費量は点Cから点Bに減っていることが読み取れます。
所得が増えたにもかかわらず、消費量が減っているので、発泡酒は下級材であると読み取ることができるわけですね。
以上のように、グラフの点Bと点Cの位置関係がどのようになっているかで、上級財・中級財・下級財が判別できますので、是非グラフの読み取り方をマスターしていただければと思います。
ギッフェン財とは?
それでは今回のメインテーマである、ギッフェン財について解説していきたいと思います。
ギッフェン財とは、価格効果よりも所得効果が大きくなるような下級財のことをいいます。
下級財であると言うところがポイントですね。
グラフ描いてみると、以下のようになります。

点Aから点Bへの消費量の変化は、代替効果を表しているのでした。
そして、点Bから点Cへの変化は所得効果を表しているのでしたね。
グラフを読み取ってみると、代替効果によって、発泡酒の消費量は点Cに増えていますが、所得効果によって、点Cから点Bに大きく消費量が減っています。
これは、もともとの消費量の点Aよりも、消費量が減っていると読み取れますね。
このような財をギッフェン財と言うわけです。
ポイントは、所得が増えると消費量が減る下級財であるということ、その消費量の減り方は代替効果よりも大きいと、ギッフェン財と呼ぶわけですね。
ギッフェン財は超下級財とも呼ばれています。
あくまで下級財の一部であるということを覚えておきましょう。
過去問を解いてみよう (平成24年度 第17問)
それではここまでの内容を、過去問解いて復習してみたいと思います。
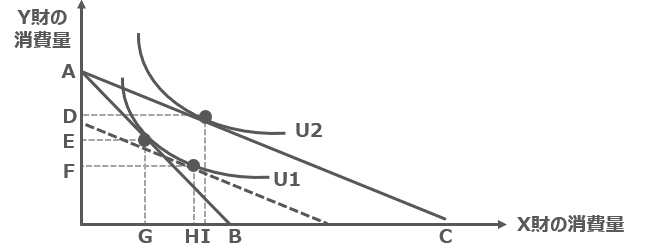
下図は、2つの財(X財とY財)のみを消費する消費者の効用最大化行動を描いたものである。当初の予算制約線はABで与えられ、効用を最大にする消費量の組み合わせは、無差別曲線U1との接点すなわち座標(G.E)として与えられている。
このとき、X財の価格が下落し予算制約線がACへと変化すると、効用を最大にする消費量の組み合わせは無差別曲線U2との接点すなわち座標(I,D)へと変化する。 なお、補助線(破線)は、予算制約線ACと同じ傾きを持ち、無差別曲線U1と接するものとする。ア X財に生じた所得効果は線分HIの長さで測られ、Y財に生じた所得効果は線分EFの長さで測られる。
イ X財の価格の低下は、X財の消費量の減少を引き起こしている。
ウ X財はギッフェン財である。
エ Y財に生じた所得効果の絶対値は、Y財に生じた代替効果の絶対値よりも大きい。
オ 座標(H,F)の効用水準は、座標(G,E)の効用水準よりも低い。
中小企業診断士試験 経済学 平成24年度第17問
いつも通りのグラフの読み取り問題ですね。
✅選択肢ア
X財に生じた所得効果は線分HIの長さで測られ、Y財で生じた所得効果は線分EFの長さで測られるとあります。
X財の所得効果に関する記述は正しいことがわかりますね。
一方で、Y財に生じた所得効果は、グラフを読み取ってみると線分FDで表されることがわかります。
ですので、選択肢アは誤りであるとわかりますね。
✅選択肢イ
X財の価格低下はX財の消費量の減少を引き起こしているとあります。
グラフを読み取ってみると、X財の消費量は、GからIに増えていることが読み取れますので、選択肢イも誤りとなります。
✅選択肢ウ
X財はギッフェン財であるとありますが、X材は所得効果によって消費量がHからIに増えているので、上級財であると読み取れますね。
ギッフェン財は下級財であるため、選択肢ウも誤りであることがわかります。
✅選択肢エ
Y財に生じた所得効果の絶対値は、Y財に生じた代替効果の絶対値よりも大きいとあります。
グラフを読み取ってみると、Y財に関する代替効果は線分EF、所得効果は線分DFとなりますので、明らかに所得効果の方が大きいことが読み取れます。
ですので、選択肢エが正解となりますね。
✅選択肢オ
座標(H,F)の効用水準は座標(G,E)の効用水準よりも低いとあります。
2つの点を見てみると、同じ無差別曲線上の点であると読み取れますね。
同じ無差別曲線上の点は効用水準が全て等しいのでした。
ですので、選択肢オも誤りとわかりますね。
いかがでしたでしょうか?
この問題は、効用や無差別曲線、スルツキー分解を正しく理解して、グラフの読み取りまで正確に行える必要があります。
一つ一つの理論の理解をコツコツ積み上げていけば、そこまで難しい問題ではないので、
ご自身の理解が足りてないと思う箇所があれば、過去の動画を見直して復習いただければと思います。

まとめ
それでは最後にまとめです。
今回は上級財・中級財・下級財、そしてギッフェン財の特徴を学習しました。
- 上級財
所得が増えたら消費量が増える財 - 中級財
消費が所得が増えても消費量が変わらない財 - 下級財
所得が増えたら消費量が減る財 - ギッフェン財
下級財のうち、価格効果よりも所得効果が大きくなるような財
本試験では、これらの用語の定義を知っているだけでなく、グラフを正確に読み取れる必要がありますので、実際にご自身でグラフを描いてみるなどして、マスターしていただければと思います。
というわけで、今回はギッフェン財について解説してみました。
試験直前になると、ギッフェン財は捨て問にすると言う受験生がチラホラと見受けられます。
しっかりと理解しておけば、そんなに難しいことをしているわけではないので、この時期から得意論点にしていただければと思います。
それでは今回の解説記事はここまでとしたいと思います。
ここまでご覧いただき、ありがとうございました。
それではまた次回の解説記事でお会いしましょう。勉強頑張ってください!応援しています。さようなら!!