はい、どうも中小企業診断士のたかぴーです!
今回は損益分岐点分析をテーマに解説していこうと思います。
初めて学習する方にもわかりやすい内容となっていますので、是非最後までご覧ください。
宜しくお願いします。
▼YouTube動画でも解説中!
損益分岐点売上高とは?
損益分岐点売上高とは、利益が0になるような売上高のことです。
このように聞くと、なんだか違和感がありますよね?
例えば1個80円で仕入れたお菓子を、お店で120円で販売したとすると、利益は40円残ります。
お菓子が1個も売れない限り、売れれば売れるほど、利益は出るはずです。
一体どういうことなのでしょうか?
この疑問を解決するのが、固定費という概念です。
この固定費があるために、例え商品が売れたからといっても、すぐに利益が出るとは限らなくなります。
費用を分解してみよう
固定費について、もう少し詳しく説明します。
皆さんご承知と思いますが、売上高 – 費用で利益を求められます。
このうち費用は、変動費と固定費に分解ができます。
変動費とは販売数に応じて増加する費用のことで、固定費は販売数によらず一定額発生してしまう費用のことです。
具体例を見てましょう。
ここでは、あなたが自動販売機ビジネスを始めるとします。
| 売上高 | 商品単価 | @100円 |
| 変動費 | 商品原価 | @60円 |
| 固定費 | 電気代 | 月5,000円 |
| 人件費 | 月10,000円 |
商品単価を1本100円に設定して、変動費としての商品原価は1本60円かかるとします。
販売数に依らず発生する固定費は、電気代が月5,000円、商品の入れ替えや自販機のメンテナンスを依頼するので、人件費が月1万円かかるとします。
そうすると、固定費は合計で月1万5,000円かかる計算ですね。
これがもし仮にジュースが1本も売れなくても発生してしまう費用となります。
これをグラフに描いて確認してみましょう。
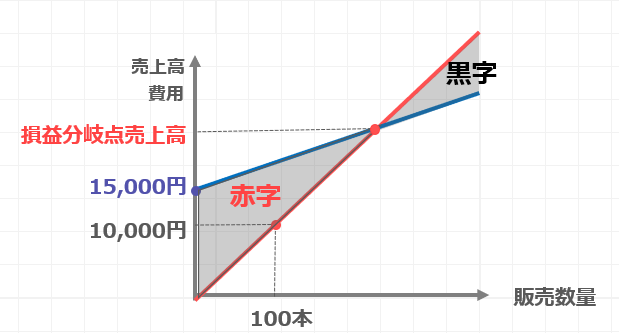
横軸に販売数量、縦軸に売上高と費用を取りました。
売上高は1本も売れなければ0円なので、原点を通る直線となります。
例えばジュースが100本売れたとすると、商品単価は100円なので、
100×100で1万円になる計算ですね。
費用についても同じグラフで考えてみます。
固定費は販売数量がゼロでも発生してしまうので、販売数量ゼロで1万5,000円がかかります。
その後、1本売れるごとに変動費としての商品原価60円が発生するので、15,000円から始まる、上記のような青色の直線となります。
赤色の売上高の直線より、青色の費用の直線が上にある領域は、売上より費用の方が高いと読み取れますので、赤字となります。
逆に赤色の直線が青色の直線を超えれば、黒字となります。
これで固定費があるせいで、一定の売上高がないと黒字化しないことが理解できたかと思います。
変動費率とは?
損益分岐点売上高の具体的な計算式を確認する前に、変動費率という考え方を説明します。
変動費率を使うことで、売上高から変動費を計算できるようになります。
先ほどの数値を使って確認してみましょう。

もし仮にジュース1本売れたら、売上高は100円、変動費は60円となりますね。
この時、変動費は売上高の60%と計算できます。
次に、5本売れたとき、30本売れたときを確認しても、変動費は売上高の60%となります。
このように、変動費は売上高に一定の係数を掛けることで計算することができます。
今回は売上高の60%が変動費となりました。
この60%の部分を、変動費率といいます。
変動費率は、変動費÷売上高で計算できますが、診断士の試験対策上は価格比で覚えておいた方が、計算が楽な場合が多いです。
損益分岐点売上高の計算式
それでは損益分岐点売上高の計算式を確認してみましょう。
損益分岐点売上高は、売上高から費用を引いて、ちょうど利益が0円になるときの売上高のことでした。
費用は変動費と固定費に分けられるのでしたね。
ここで変動費を先ほどの変動費率を使って表してみますと、
売上高 – 変動費 – 固定費 = 利益0
⇔売上高 – 変動費率 × 売上高 – 固定費 = 0
⇔S – αS – FC = 0
という式に変換できます。
これが損益分岐点売上高の公式となりますので、覚えておきましょう。
毎回日本語で書き起こすの面倒なので、売上高はS、変動費率はα、固定費はFCで表すことが多いですね。
それでは先ほどの自販機の例を使って、実際に損益分岐点売上高を計算してみましょう。
売上高S – 変動費率$\frac{60}{100}$×S-固定費15,000=0
⇔$\frac{40}{100}$×S=15,000
⇔S=15,000×$\frac{100}{40}$
⇔S=37,500 ← 損益分岐点売上高
計算すると、S=37,500円となります。
これが損益分岐点売上高になるわけですね。
試験対策上、損益分岐点売上高を計算する時は、分数は分数のままで残して最後に計算することをお勧めします。
途中で小数点にしてしまうと、思わぬ計算ミスをしてしまったり、数値が割り切れない時には、計算結果が合わないことがあるためです。
損益分岐点比率・安全余裕率とは?
続いて、損益分岐点比率と安全余裕率という考え方をご説明します。
診断士試験で問われることがありますので、この機会にぜひ覚えてください。
まず損益分岐点比率は、損益分岐点売上高÷実際の売上高で計算できます。
売上高を横軸に取った図に書いてみるとわかりやすいです。

先ほどまでの例で、損益分岐点売上高は37,500円でした。
今月は頑張って月500本ジュースを売ることができて、売上高が50,000円だったとしましょう。
この時、損益分岐点比率は37,500÷50,000円で75%と計算できます。
図で表すと、売上高の75%の位置に損益分岐点があるということになりますね。
この損益分岐点比率を計算することで、売上高と損益分岐点がどれだけ近いかを確認することができます。
当然、100%に近づくほど赤字ギリギリの売上高だと判断することができます。
一方で、余裕率は100%から損益分岐点比率を差し引くことで計算できます。
実際に計算してみると、100%-75%で、25%と計算できます。
図で示すと、青色の範囲となりますね。
安全余裕率は、損益分岐点売上高に対して実際の売上高がどれくらい余裕があるかを表しますので、
100%近づくほど、売上減少リスクに強いと読み取ることができます。
まとめ
いかがでしたでしょうか?
今回は損益分岐点売上高分析の方法を解説しました。
この論点は、二次筆記試験でも出題されますので、多少時間をかけてでも、しっかりとマスターするようにしましょう。
それでは今回の解説記事はここまでとしたいと思います。
ここまでご覧いただき、ありがとうございました。
それではまた次回の解説記事でお会いしましょう。勉強頑張ってください!応援しています。さようなら!!