はい、どうも中小企業診断士のたかぴーです!
今回は現在価値をテーマに解説していきたいと思います。
診断士試験の重要論点である正味現在価値法の基礎にあたる部分ですので、この記事でしっかりと考え方を覚えていただければと思います。よろしくお願いします。
▼YouTube動画でも解説中!
現在価値とは?
まず最初に結論からお見せしますと、現在価値は以下の計算式で表されます。
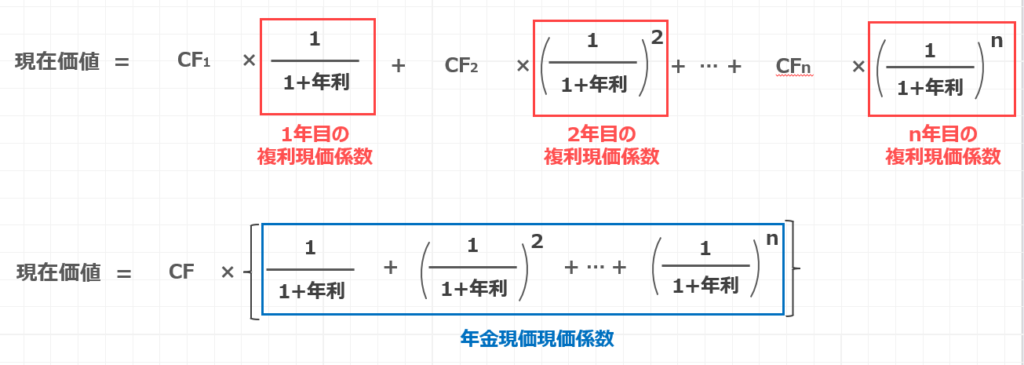
赤色で囲った部分が複利現価係数、青色で囲った部分が年金現価係数と呼ばれます。
かなり数式が複雑ですし、何をやっているかも分かりにくいので、これから丁寧に解説していこうと思います。
今すぐもらえる100万円と来年の100万円の評価
さて、突然ですが、ここでひとつ質問です。
今すぐ100万円を貰えるのと来年101万円がもらえるの、どちらが嬉しいでしょうか?
皆さんだったらどう答えますかね?
答えを言いますと、財務・会計の世界では今すぐ100万円もらえる方が嬉しいと答えて欲しいところです。
額面上は来年の101万円の方が多いのに、どうしてこのような答えになるのでしょうか?
これは時間経過で、今もらえる100万円の価値が変わるためです。
詳しく解説していきます。
今すぐもらえる100万円の評価
それでは、今すぐもらえる100万円について評価をしてみましょう。
条件としては今すぐ100万円もらえるか、来年101万円もらえるかでしたね。
そしてもう一つ条件として定期預金に預けることで、年利10%でお金が増えていくとしましょう。
図に表すと、以下のようになります。
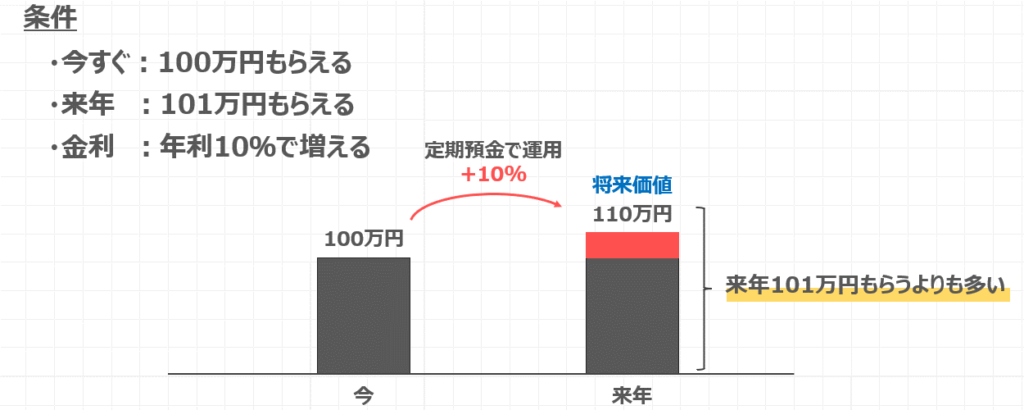
今すぐ100万円もらえて、定期預金で運用すると10%増えて110万円になりますね。
ちなみに、この110万円のことを将来価値と言います。
この将来価値である110万円は来年101万円もらうよりも金額としては大きいので、やはり今すぐ100万円もらえた方がお得感があると言うことになりますね。
財務会計の世界では、このように金利を考慮に入れながら、同じ時間軸で金額を評価します。
初めて金融の勉強する方は慣れないかもしれませんが、頑張ってついてきてください。
来年もらえる101万円の評価
先ほどは時間軸を来年に合わせて比較しました。
今度は逆に来年もらえる101万円というのは、今現在に直すと何万円分の価値になるかを考えてみましょう。
条件は先ほどと同じです。
今もらえるお金を仮にX万円とおきました。
これを同じように先ほどと同じように、年利10%の定期預金で運用したとして来年101万円に増えると考えます。
この時のX万円がいくらになるのかを考えてみましょう。
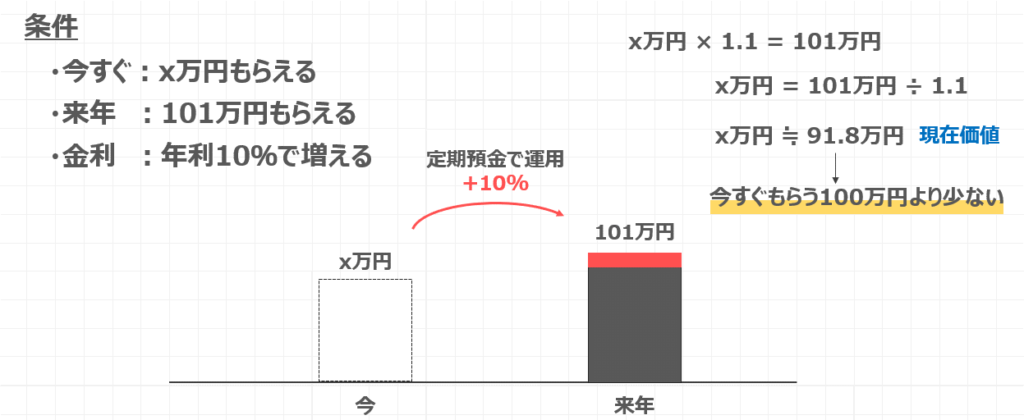
数式で表すと、X万円×1.1=101万円と書くことができますね。
ここからは単純な数学の問題です。実際に計算してみましょう。
X万円×1.1=101万円
⇔X万円=101万円÷1.1
⇔X万円≒91.1万円 ← 現在価値
この時の91.8万円のことを、現在価値と呼びます。
この現在価値91.8万円は、今すぐもらう100万円よりも少ないので、
やはり来年101万円もらうよりも、今すぐ100万円もらった方が良いということがわかりますね。
将来価値で比較しても、現在価値で比較しても今すぐ100万円もらう方がお得だということがわかりました。
現在価値の求め方
それでは現在価値の求め方について、改めて確認をしていきましょう。
先ほどはこのようにX万円とおいて、それが10%で増えることを想定しました。
計算式ではX万円を求めるために101万円を1.1で割り返しています。
これを図で表すと101万円に1+0.1分の1をかけていることになります。
将来もらえるお金に1+金利分の1を掛けることで、現在価値が求まるわけですね。
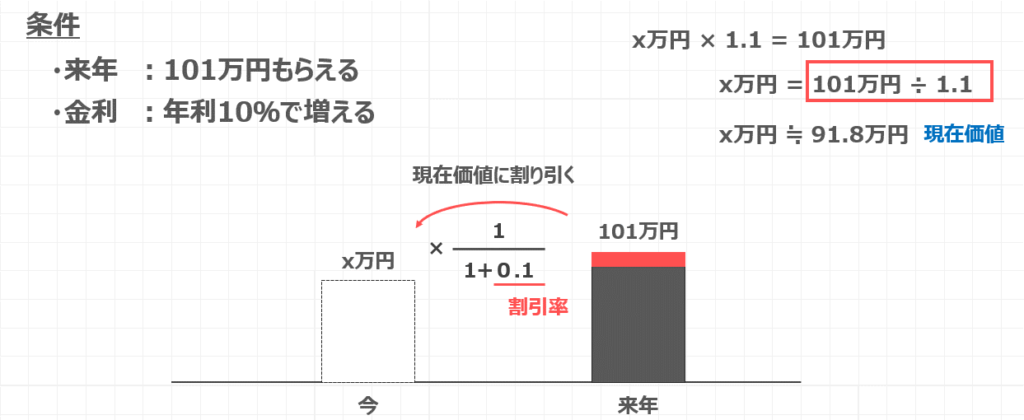
ちなみに、この来年のお金に$\frac{1}{1+金利}$を掛けることを、現在価値に割り引くといいます。
そしてこのときの金利のことを割引率といいますので、覚えておきましょう。
複数年にわたる現在価値の求め方
来年と2年後の両方ともお金をもらえる場合の現在価値についても考えてみましょう。
条件として1年後に50万円、2年後に100万円もらえるとします。
年利は先ほどまでと同じ10%とします。
図で表わすと、現在価値をX万円とおきまして、1年後に50万円もらえるのでこれを現在価値に割り引くには、50万円に$\frac{1}{1+0.1}$をかけるのでしたね。
これは先ほどまでと同じです。
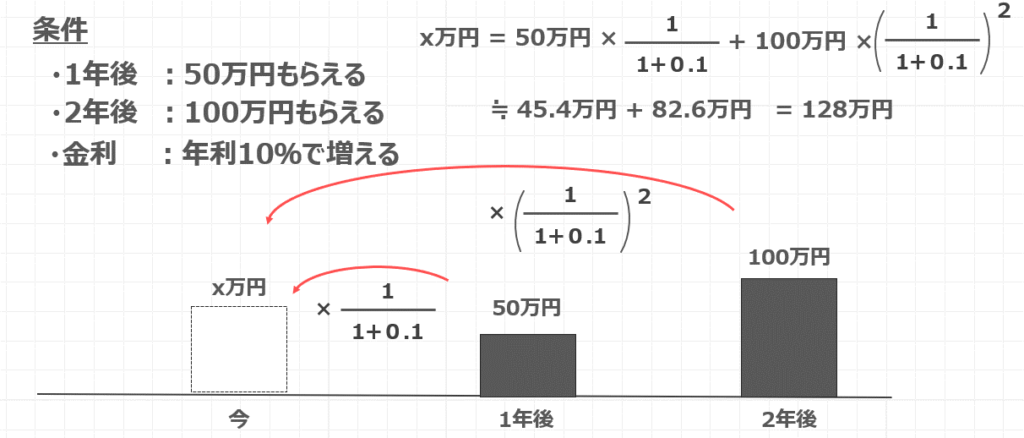
そして、2年後にもらえるお金に対しては2年間という時間を考慮して、$\frac{1}{1+0.1}$2をかけるのでした。
このようにして、1年後と2年後もらえるお金それぞれに係数をかけてあげる必要があるわけですね。
そして、これらの合計が求めたい現在価値となります。
数式で表すと、このような形となりまして、これを計算すると、45.4万円+82.6万円となって、この合計が128万円となります。
以上のように、複数年でお金がもらえる場合は、お金がもらえるタイミングに応じた係数を掛けてあげて、それらを合計することで現在価値が求まります。
現在価値の求め方と複利現価係数
それではここで、現在価値の公式について確認してみましょう。
現在価値は1年後にもらえるお金に$\frac{1}{1+年利}$を掛けて求まるのでした。
さらに2年後にもお金がもらえる場合は、2年後にもらえるお金に、$\frac{1}{1+年利}$2を掛けてから合計するとよいのでしたね。
2年後は2乗、3年後は3乗になるのがポイントでした。
さらにもらえる年数が増えて、n年後にもお金がもらえるとすると、n年後のお金に$\frac{1}{1+年利}$nを掛けて合計する必要があります。
これが、現在価値の求め方の公式となります。
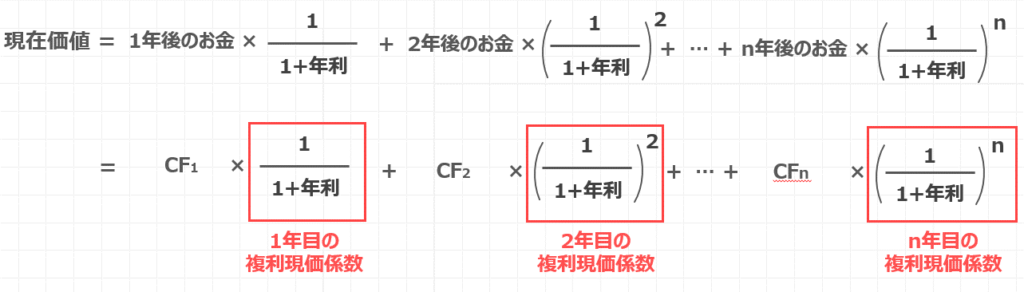
何年後にもらえるお金と毎回書くのは煩わしいので、テキストなどではもらえるお金をキャッシュフローと呼んで、このように頭文字のCFで表すことが多いです。
ここで用語説明です。
1年目$\frac{1}{1+年利}$の部分を1年目の複利現価係数、2年目のものは2年目の複利現価係数と呼びます。
この用語は試験問題でも当然知っているものとして出題されますので、覚えておいてください。
年金現価係数とは?
用語説明の2つ目として、年金現価係数も説明したいと思います。
もし仮に毎年もらえるキャッシュフローが同額だったとしましょう。
その時、CFが同額なので括弧でまとめることができます。

この括弧の中身の青色で囲った部分が、年金現価係数となります。
毎年もらえるキャッシュフローが同じ場合、各年の複利現価現価係数の合計値が、年金現価係数と呼ばれるわけですね。
それぞれの違いも合わせて、よく覚えておきましょう。
まとめ
最後にまとめです。
現在価値は、以下の数式で表されるのでした。
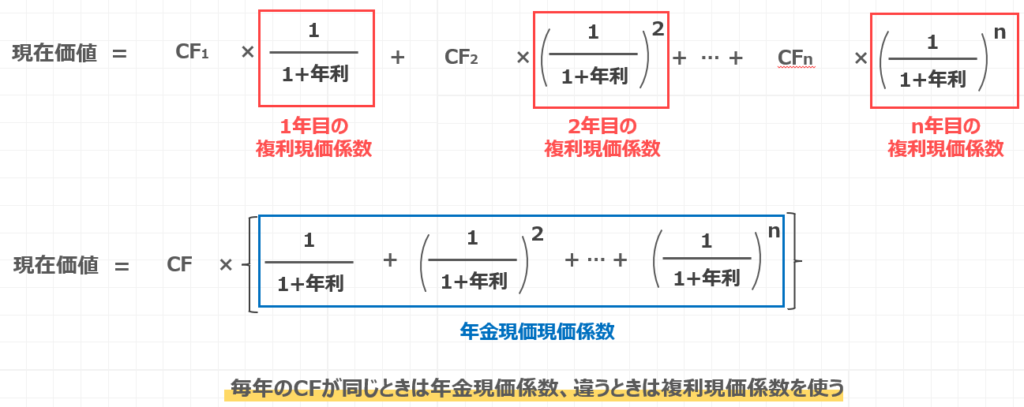
そして、赤枠で囲った部分が複利現価係数でしたね。
青枠で囲った部分が年金現価係数でしたね。
毎年のキャッシュフローが同じときは年金現価係数、そうでないときは、複利現価係数を使うというように覚えていただければと思います。
それでは今回の解説記事はここまでとしたいと思います。
ここまでご覧いただき、ありがとうございました。
それではまた次回の解説記事でお会いしましょう。勉強頑張ってください!応援しています。さようなら!!




























