はいどうも、中小企業診断士のたかぴーです。
今回はリスク・プレミアムと確実性等価について解説していきたいと思います。
リスク・プレミアムの計算はやや複雑なので、苦手意識を持っている方も多いのではないでしょうか?
かくいう私も、受験生時代は苦手論点の一つでした。
今回で得意論点にできるよう、丁寧に解説できればと思いますので、ぜひ最後までご覧いただければと思います。
リスク回避的投資家とリスク愛好的投資家の違い
まずはリスク回避的投資家と、リスク愛好的投資家の違いについてです。
リスク回避的投資家は、所得が増えるほど効用の上昇量が減る投資家のことをいいます。
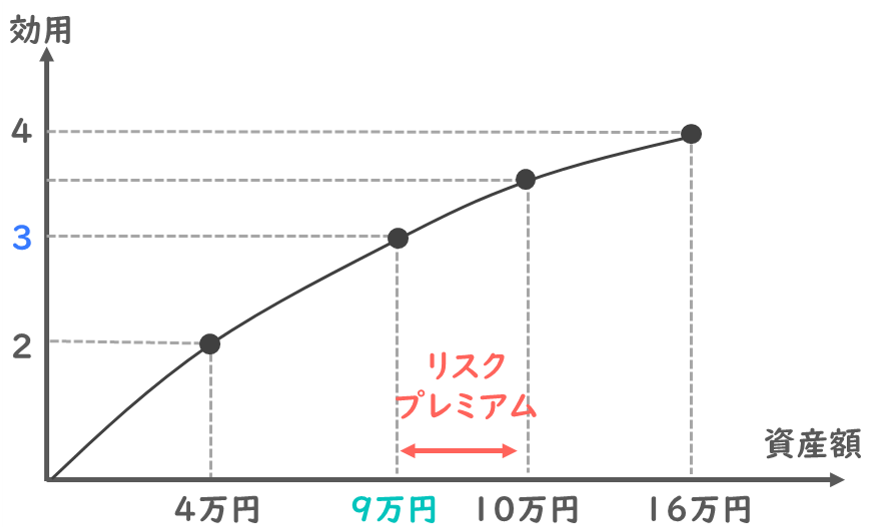
例えば、横軸に所得とリスクを、縦軸に効用を取った場合、リスク回避的な投資家の所得と効用の関係は、次のようなグラフで表されます。
グラフの中身を見てみますと、所得が低い状態の時は、所得が2単位増えると効用が2単位増えていますが、次に同じように所得が2単位増えても、効用は1単位しか増えていないことがわかります。
つまり、所得が増えるたびに、効用の増加量が減っていっていることが読み取れますね。
一方、リスク愛好的投資家は、所得が増えるほど効用の上昇量が増えるような投資家をいいます。
同じようにグラフ化してみますと、所得が低いときの時は所得が2単位増えると、効用が2単位増えていますが、さらに所得が2単位増えたときに効用が4単位増えていることが読み取れますね。
このようにリスク愛好的投資家は所得リスクが増えると、その分だけ効用が増えるので、どんどんリスクを追って所得は増やすという行動をとります。
基本的に経済学で消費者行動を考えるときは、リスク回避的投資家を前提として考えます。
子供の時にもらったお小遣い500円はとても嬉しいものでしたが、ある程度所得のある大人が500円もらったとしても、そこまで喜びを感じないことからも、ほとんどの人がリスク回避的投資家であることが納得いただけるかと思います。
今回学習するリスク・プレミアムも、リスク回避的投資家を前提として考えておきますので、最初に解説しておきました。
確実性等価とリスク・プレミアムとは?
それでは本題の確実性等価とリスク・プレミアムについて説明したいと思います。
リスク・プレミアム
リスク・リスクプレミアムとは、リスクに対して納得感を得られるだけのリターンのことを言います。
例えば今、次の2つの投資案があったとします。
A. 確実に9万円もらえる投資
B.半々の確率で4万円か16万円もらえる投資
この2つの投資案件の期待収益は、どれだけ違うでしょうか?
Aの期待値は、4万円×確率50%+6万円×確率50%=10万円と計算ができますね。
リスク・プレミアムは、この期待値10万円と9万円の差分のことを言います。
リスク・プレミアムは、リスクに対して納得感を得られるだけのリターンなので、確実に9万円もらえる状況にありながら、リスクを負うのだとしたら、期待値として+1万円は増えないと納得感を得られないということが言えるわけですね。
確実性等価
それでは、確実性等価という用語も確認したいと思います。
ここで、Aの効用とBの期待効用が同じだという前提を置いてみましょう。
A. 確実に9万円もらえる投資
B.半々の確率で4万円か16万円もらえる投資
→ Aの効用とBの期待効用が同じと考える!
期待効用とは、4万円の効用と16万円の効用の期待値を指します。
この時、Bの9万円を確実性等価と言って、Aの期待値10万円と確実性等価の差分のことをリスク・プレミアムといいます。

文章だけだとわかりにくいので横軸に資産額、縦軸に効用を取ったグラフで考えていきたいと思います。
今、4万円がもらえる時の効用が2、16万円の効用が4だったとします。
この時の期待効用を計算すると、4万円の効用2×確率50%+16万円の効用4×50%で3と計算ができますね。
ここまで分かると、確実性等価が計算できます。
確実性等価とは「Bの期待効用」と「効用の値が等しい確実にもらえる資産額」と定義されています。
つまり、今計算した期待効用3と一致するような資産額9万円が、確実性等価となるわけですね。
そしてこの確実性等価9万円と、Aの期待値10万円の差分がリスク・プレミアムだと定義されています。
確実性等価さえ計算できれば、リスク・プレミアムを求めるのは難しくありませんが、期待効用を求めてから確実性等価を求めるプロセスが少し難しいポイントなので、改めて計算方法を確認してみましょう。
リスク・プレミアムの計算方法
先ほどと同じ数値を使いながら、計算方法を確認したいと思います。
以下の問題を一緒に解いてみましょう。
効用が√xで表されるとき、半々の確率で4万円か16万円もらえるときのリスク・プレミアムを求めよ。xは、投資によって獲得できる資産額を表します。
不確実な投資案件の数値しか与えられていないので、確実性等価とこの投資の期待値を求める必要がありそうですね。
横軸に資産額、縦軸に効用を取って、図を描きながら確認していきましょう。
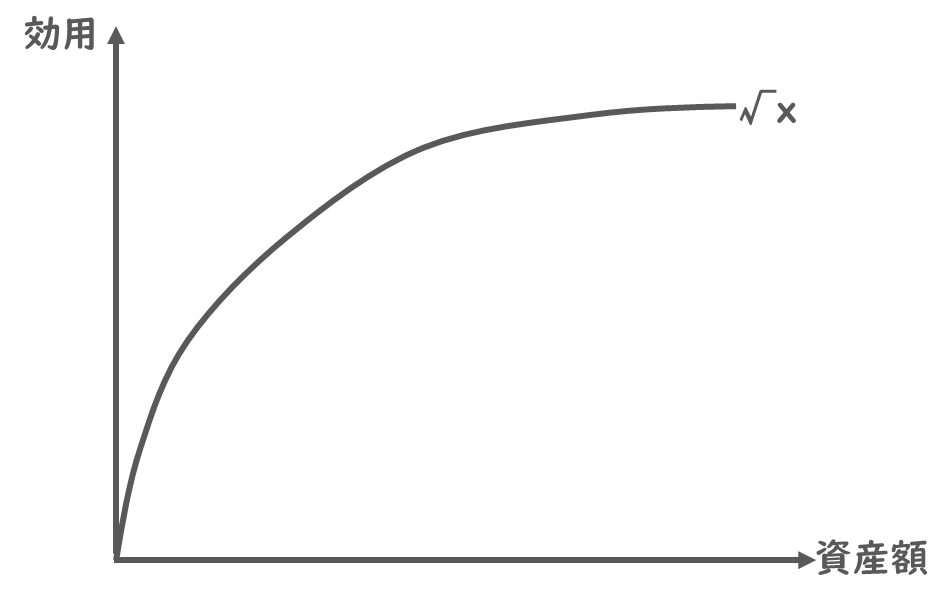
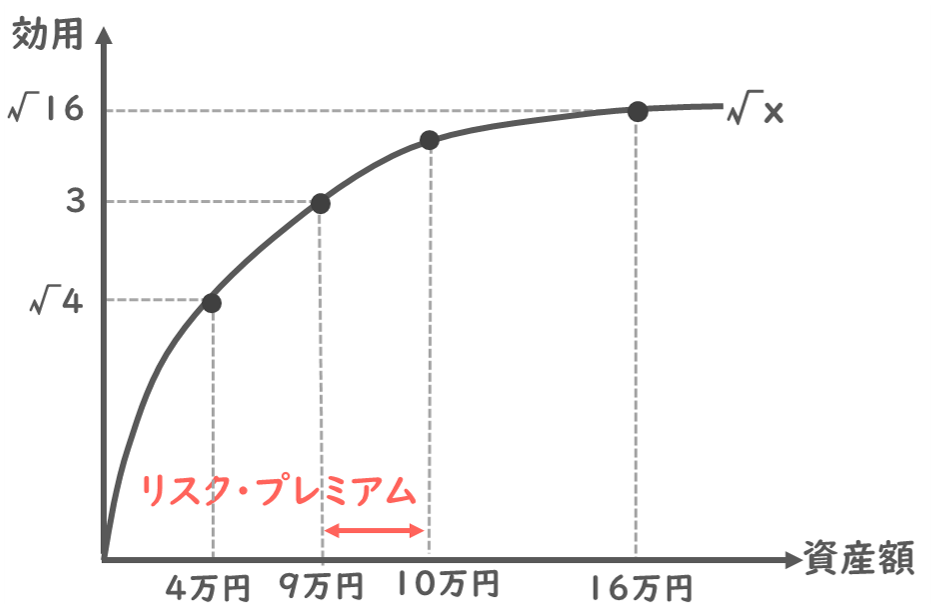
資産額と効用の関係は、√xで表されるのでしたね。
ですので、資産額4万円のときの効用は√4、6万円の時の効用は√16と置くことが出来そうです。
効用が分かったので、この投資案件の期待効用が求められそうです。
✅不確実投資の期待効用
それぞれの確率は半々であるので、期待効用は√4 ×確率50% +√16 × 50%と置くことができそうですね。
√4とは2乗して4になる数ですので、2乗して4になる数は2、2乗して16になる数は4だと計算ができます。
これを計算すると期待効用は3となりました。
✅確実性等価の効用
ここで、先ほど解説した通り、この期待効用の値と、確実性等価の効用は同じなのでした。
ですので、確実性等価の効用は3と置けそうですね。
ここまで分かれば、確実性等価を計算できます。
✅確実性等価
確実性等価の効用は、√xで表されますので、√x=3と表すことができます。
数式から√を取るには、両辺を2乗する必要があるので、両辺を2乗すると、x= 9万円と求めることができますね。
これがこの問題の確実性等価となります。
✅不確実投資の期待値
リスク・プレミアムは確実性等価と不確実な投資の期待値の差分でしたので、この投資の期待値も求める必要がありますね。
4万円がもらえる確率と16万円がもらえる確率はそれぞれ50%ですので、この期待値を計算すると、10万円となります。
以上から、リスク・プレミアムは期待値10万円−確実性等価9万円で、1万円と求められます。
図で確認すると、10万円と9万円の差が、リスク・プレミアムというわけですね。
このように、リスク・プレミアムの計算は期待効用から確実性等価を求めるという、少し回りくどい手順で行う必要がありますので、何度か問題を解きながら頭に入れていただければと思います。
よく間違いやすいケースとしては、不確実な投資の期待値の効用を求めてしまうというパターンです。
期待値と期待効用は全く別物となりますので、この点に注意いただければと思います。
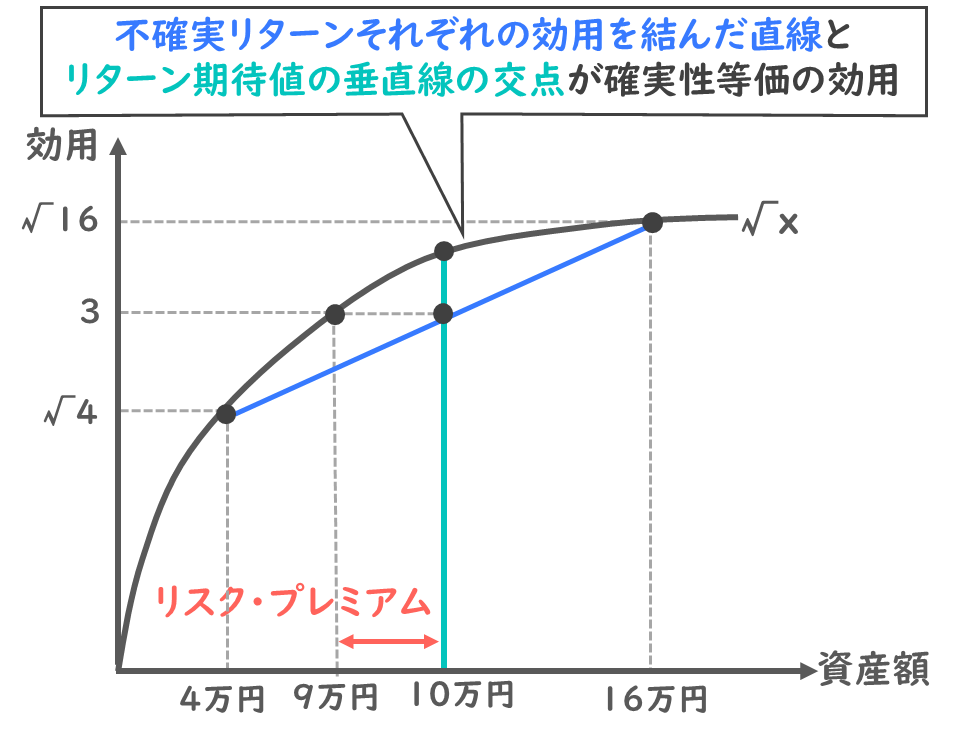
最後に、1つ重要な考え方を示したいと思います。
不確実な投資のリターンである4万円の効用と、16万円の効用値を青の直線で結びます。
また、同じく不確実な投資の期待値で、緑色の垂直線を引いてみます。
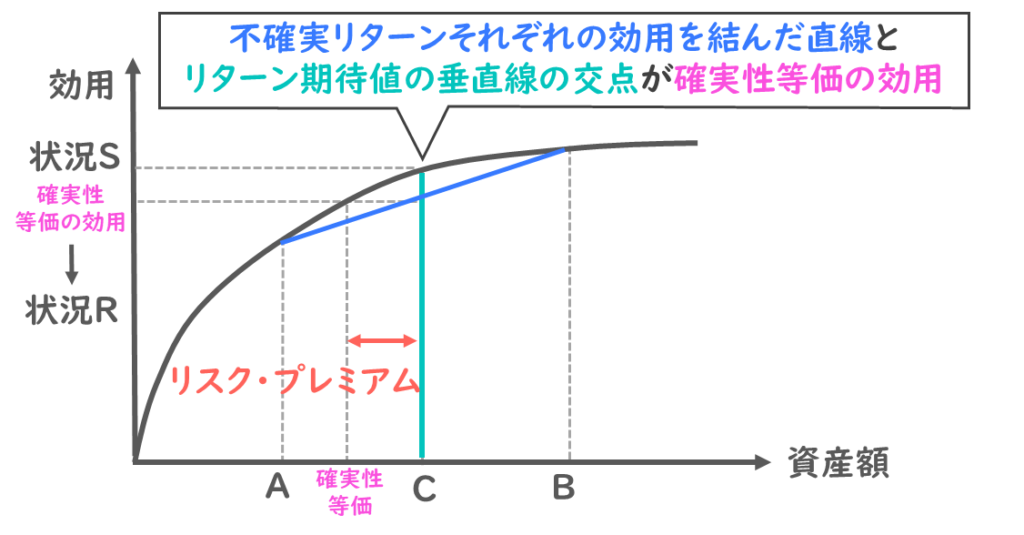
この青線と緑線の交点は、確実性等価の期待値になります。
知識として、不確実リターンそれぞれの効用を結んだ直線とリターン期待値の垂直線の交点が、確実性等価の効用とだと覚えておきましょう。
数学的に証明することもできますが、やや難しい話となりますので、この結論だけを頭に入れていただければと思います。
過去問を解いてみよう (平成26年度 第23問)
それではここまでの内容を、過去問を解いて復習してみましょう。
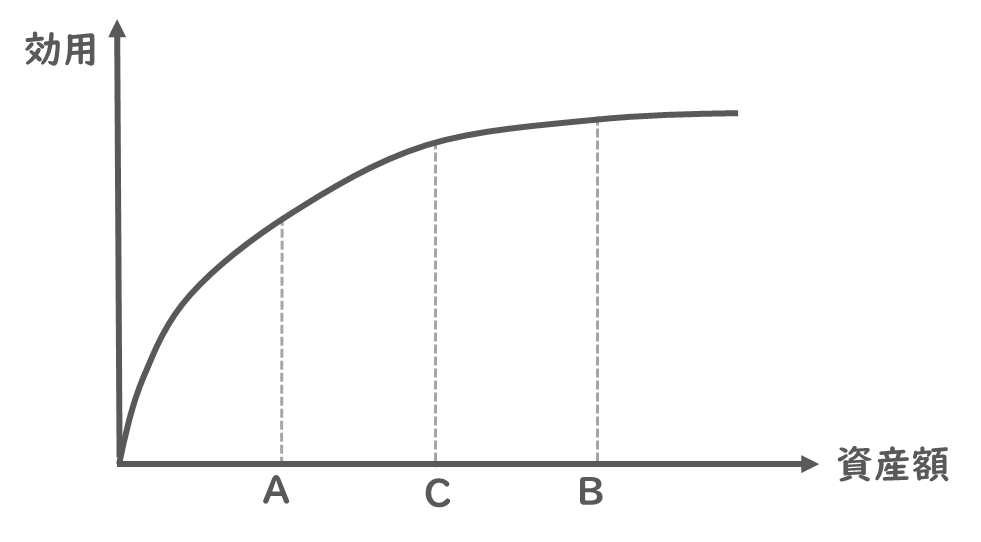
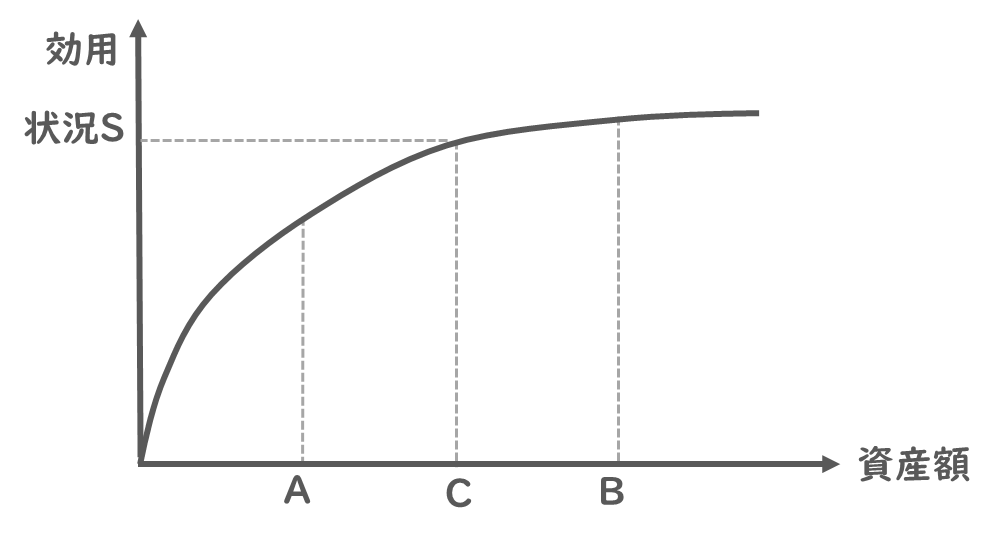
下図は、あるリスク回避的な個人における資産額と効用水準の関係を示したものである。下図で、50%の確率で高い資産額Bになり、50%の確率で低い資産額Aとなるような不確実な状況を「状況R」と呼ぶことにする。また、AとBのちょうど中間の資産額Cを確実に得られる状況を「状況S」と呼ぶことにする。「状況R」の期待効用と「状況S」の期待効用とを比較した時の説明として、最も適切なものを下記の解答群から選べ。
ア 期待効用は「状況R」の方が大きく、この個人のリスクプレミアムは正の値となる。
イ 期待効用は「状況R」の方が大きく、この個人のリスクプレミアムは負の値となる。
ウ 期待効用は「状況R」の方が小さく、この個人のリスクプレミアムは正の値となる。
エ「状況R」と「状況S」の期待効用は等しく、この個人のリスクプレミアムはゼロとなる。
中小企業診断士試験 経済学 平成26年度 第23問
問題文が分かりにくく書かれていますが、要は期待効用とリスクプレミアムの関係を見る問題ですね。
不確実な投資を状況R、確実に資産を得られる投資を状況Sと呼ぶようです。
ですので、まずは状況Sの期待効用はすぐに図から読み取れますね。
一方で、状況Rの期待効用は数字が与えられていないので計算することができません。
そこで思い出していただきたいのですが、不確実リターンそれぞれの効用を結んだ直線と
リターン期待値の垂直線の交点が、確実性等価の効用なのでした。
ですので、青線と緑線の交点が確実性等価の効用となるわけですね。
また、確実性等価の定義から、確実性等価の効用と不確実な投資の期待効用は等しいのでした。
ですので、青線と緑線の交点が状況Rの期待効用であると読み取れますね。
確実性等価の効用が分かっていますので、確実性等価も図から読み取れます。
ここまで分かれば、正解選択肢が選べそうですね。
図から期待効用は状況Rの方が小さく、リスクプレミアムは正だと読み取れますので、選択肢ウが正解となります。
この問題は緑線と青線の交点が確実性等価の効用だと分かっていないと、なかなか自信を持って正解にたどり着くのは難しい問題だったかと思います。
ぜひ、知識として覚えておいていただければと思います。
また、計算問題も出題される可能性がありますので、問題集などで忘れずに復習しておいてください。
まとめ
それでは最後にまとめです。
今回学習した用語は以下の3つです。
- リスク・プレミアム
→ リスクに対して納得感のあるリターン = 不確実な投資の期待値と確実性等価の差分 - 期待効用
→ 不確実な投資それぞれの効用の期待値 - 確実性等価
→ 「不確実性のある資産の期待効用」 と 「効用の値が等しくなるような確実にもらえる資産額
期待効用は、不確実な投資の期待値における効用ではない点がポイントなのでしたね。
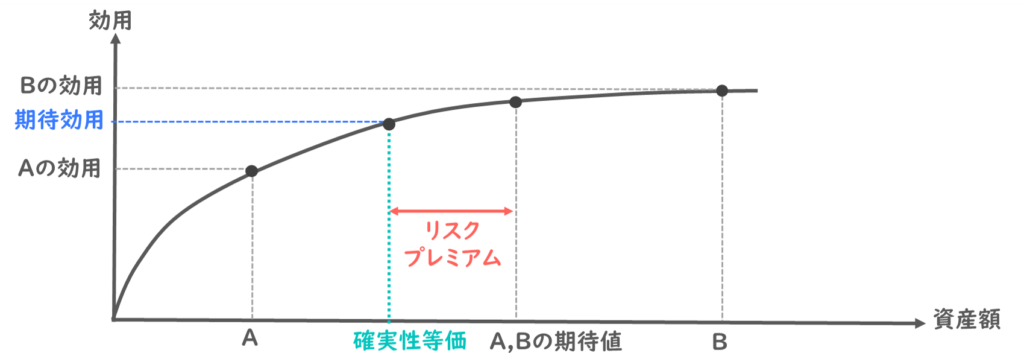
図で表すと、確率でA,Bの資産がもらえる投資があった際に、AとBの効用の期待値が期待効用で、その期待効用のときの資産額が確実性等価なのでした。
そして、A,Bの期待値と確実性等価の差がリスク・プレミアムなのでしたね。
というわけで、今回は確実性等価とリスク・プレミアムをテーマに解説してみました。
特に確実性等価と期待効用の考え方が理解しにくいところですので、記事を見返してよく復習いただければと思います。
出題頻度はそこまで高くない論点ではありますが、出題されるとほとんどの受験生が正答できない論点かと思いますので、この記事をご覧の皆さんは確実に得点につなげて、他の受験生と差をつけてくださいね。