はいどうも、中小企業診断士のたかぴーです。
今回は混合品種ラインの編成効率の計算式をテーマに解説していこうと思います。
混合品種ラインの計算式はとても複雑なので、そもそも覚えてないという方も多いのではないでしょうか?
そんな混合品種ラインの計算式を、今回解説する覚え方でバッチリ覚えられると思いますので、ぜひ最後までご覧頂ければと思います。よろしくお願いします。
▼YouTube動画でも解説中!
ライン生産とは?
まずは基礎的な内容として、ライン生産について復習しておきましょう。
ライン生産とは材料が移動するにつれて加工が進んでいく生産方式です。

カット野菜工場の生産ラインについて確認してみると、まず工程1で野菜を洗ってから、工程2で野菜を切って、工程3で袋詰めするという作業が、一つのベルトコンベアの上で行われています。
このような生産方式をライン生産と呼ぶのでしたね。
この時、各工程の所要時間はそれぞれ2分、3分、4分かかるとします。
そうしますと、各工程の所要時間の合計は2+3+4で9分となりまして、作業ステーション数は作業場所の数を表しますので、3つあるということがわかります。
編成効率の計算式
編成効率の計算式についても確認しておきましょう。
編成効率とは、生産ラインにおいてライン編成の効率性を表す指標なのでした。
具体的な計算式は以下の通りです。
編成効率=$\frac{各工程の所要時間の合計}{サイクルタイム×作業ステーション数}$
編成効率の求め方について自信がない方は、以下の動画で解説していますので、ご確認ください。
念のため簡単に触れて復習しておきますと、サイクルタイムは材料を投入する時間間隔で、
作業ステーション数は作業場所の数でした。
また、各工程の所要時間の合計は、製品を投入してから製品1個作り終わるまでの時間を表しているのでした。
ここまでが、通常のライン生産の編成効率の求め方です。
混合品種ライン生産とは?
これに対して、混合品種ライン生産はどのようになっているのでしょうか?
基本的に、先ほどの通常のライン生産と同じ設備で同じ作業をしています。
違っているのは、生産する品種の数ですね。

先ほどまではキャベツのカット野菜だけを生産していましたが、混合品種ラインではキャベツ以外にも人参や玉ねぎなど他の野菜についても加工します。
このように混合品種ラインは一つのラインに複数の品種を混合して生産する方式のことを言います。
この時、作業ステーション数は先ほどと変わらず3つですが、各工程の所要時間が変わります。
野菜によって洗う時間や切る時間が変わってきますからね。
キャベツは9分、人参は8分、玉ねぎは10分というように、品種ごとに加工時間が変わっていきます。
これで混合品種ライン生産のイメージはつかめたかと思います。
混合品種ラインの編成効率の計算式
それでは今までの内容を踏まえて、混合品種ラインの編成効率の計算式を確認してみましょう。
多くのテキストで書かれている計算式は以下の通りです。
混合品種ラインの編成効率=$\frac{各製品の(生産量×総作業時間)の合計}{ステーション数×サイクルタイム×各製品の生産量合計}$
例えばこのようなケースを考えてみましょう。
ステーション数が3つで、サイクルタイムが4分、各種製品の総作業時間と生産量が書かれた表があります。
| カット野菜工場 | キャベツ | にんじん | たまねぎ |
|---|---|---|---|
| 総作業時間(1個あたり) | 9分 | 6分 | 7.5分 |
| 生産量(1ヶ月あたり) | 200個 | 100個 | 100個 |
これに先ほどの編成効率の計算式を当てはめると、以下のようになります。
混合品種ラインの編成効率=$\frac{200個×9分+100個×6分+100個×7.5分}{3つ×4分×(200個+100個+100個)}$
この計算式だと何をやってるか全然分からないですよね。
結果、多くの受験生は何をやっているのか分からないまま、この計算式を丸暗記しようとして、試験本番に忘れてしまうのが実情だと思います。
そこで今回は、この計算式がどのようにして導かれているのかを解説していきたいと思います。
結論を言いますと、混合品種生産ラインの編成効率は、各製品の編成効率の生産量に応じた加重平均だと覚えていただければと思います。
これだけだと分からないと思うので、詳しく中身を見ていきますね。
加重平均とは?
まずは加重平均について確認してきましょう。
事例を用いながら解説していきたいと思います。
キャベツ・にんじん・玉ねぎのカット野菜工場について考えていきます。
カット時間はそれぞれキャベツが1分、人参も1分、玉ねぎが10分だとします。
また、生産量はキャベツは10個、にんじんも10個、玉ねぎを100個作っているとしましょう。

それでは、この工場全体でのカット時間の加重平均はいくつになるでしょうか?
加重平均を求める際は、生産量を加味して平均値を出していく必要があります。
キャベツの1分に対して、全体の生産量120個のうち、キャベツの生産量は10個ですので、10/120を掛けます。
また、にんじんについても10/120を掛け、玉ねぎは100個作ってますので100/120を掛けます。
そして、これらの合計しますと、約8.5分と計算できます。
こうすることで、それぞれの生産量に応じて重みづけをした平均値を取ることができました。
このような平均値の取り方を加重平均と呼ぶわけですね。
ここで計算した8.5分という平均値も、直観に近いかと思います。
編成効率の生産量に応じた加重平均
それでは編成効率の生産量に応じた加重平均についても確認してみましょう。
考え方は先ほどのカット時間の平均値と同じです。
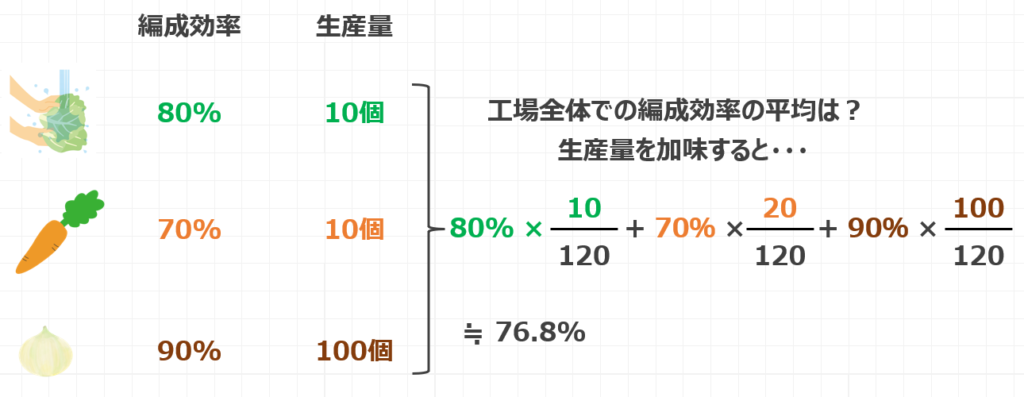
上記のカット野菜工場において、編成効率がこのように決められているとしましょう。
この工場全体での編成効率の平均値はいくつになるのでしょうか?
これを計算する時も、生産量を加味して重み付けした方が良さそうですよね。
計算式としては、以下のようになります。
混合品種ラインの編成効率=80%×$\frac{10}{120}$+70%×$\frac{20}{120}$+90%×$\frac{100}{120}$
それぞれの編成効率に対して生産量に応じた重み付けをしてあげます。
分数で表している部分が重みづけにあたります。
これを計算すると76.8%となるわけですね。
これが混合品種ラインの編成効率の求め方となります。
考え方がわかると、意外と大したことをしていないことが分かったのではないでしょうか?
過去問を解いてみよう (平成25年度 第9問)
それではここまでの内容を、過去問を解いて復習してみましょう。
混合品種組み立てラインの編成を検討した結果、サイクルタイムを150秒、ステーション数を10とする案が提示された。生産される3種類の製品A、B、Cの総作業時間と1ヶ月当たりの計画生産量は、以下の表に与えられている。この案の編成効率に最も近い値を求めよ。
中小企業診断士試験 運営管理 平成25年度 第9問
製品A 製品B 製品C 総作業時間(秒/個) 1,400 1,450 1,450 生産量(個/月) 2,000 1,000 1,000
サイクルタイムは150秒、ステーション数は10と文章題に記載されていて、各製品の総作業時間と生産量が表で与えられていますね。
まずは各製品の編成効率を求めてみましょう。
$\frac{1,400秒}{ステーション数10×150秒}$=$\frac{140}{150}$
$\frac{1,450秒}{ステーション数10×150秒}$=$\frac{145}{150}$
$\frac{1,450秒}{ステーション数10×150秒}$=$\frac{145}{150}$
この分数を計算してしまうと後々大変になりますので、分数のままで残しておきます。
製品Cの編成効率も製品Bと全く同じとなりました。
そして表の生産量の割合について見てみますと、各製品の生産量の合計は4,000で、そのうち製品Aは2,000作られていますので、計算すると2/4が製品Aの生産に当てられているとわかりますね。
製品B・Cについては、それぞれ1/4ずつということがわかります。
これを踏まえて編成効率に生産量に応じた重み付けをしましょう。
$\frac{140}{150}$×$\frac{2}{4}$+$\frac{145}{150}$×$\frac{1}{4}$+$\frac{145}{150}$×$\frac{1}{4}$=$\frac{570}{600}$=95%
実際に計算しますと95%となります。
これがこの問題の答えですね。
いかがでしたでしょうか?そんなに難しくはなかったですよね。
混合品種ラインの編成効率の問題は、ほかの受験生の方はかなり苦労すると思いますが、この記事をご覧の皆さんは、鼻歌を歌いながらでも問題を解けるようになったかと思います。
まとめ
それでは最後にまとめです。
混合品種ラインの編成効率は、各製品の編成効率の生産量に応じた加重平均と覚えてください。

具体的な例で見てみますと、各製品の編成効率と生産量に基づいて、この工場全体での編成効率を求めるときには、各製品の編成効率に対して、生産量に応じた重み付けをしてあげます。
これらを足し合わせた値が混合品種ラインの編成効率となるわけですね。
確かに今回解説した計算式は、計算式自体がかなり長くなってしまいます。
テキストで解説されている計算式は今回紹介した計算式を変形して、素早く計算することに特化した計算式となっています。
計算が早くなる一方で、計算式を見ただけでは何をやってるのかが分からなくなっているというデメリットがあります。
結果的に、計算式自体を忘れてしまうという受験生が多発します。
ですので、まずは今回ご紹介した計算式を覚えていただいて、試験本番で計算式を変形しながら解いていけるのが理想的ですね。
繰返し問題を解きながら混合品種ラインの編成効率についてもマスターしていきましょう。
それでは今回の解説記事はここまでとしたいと思います。
ここまでご覧いただき、ありがとうございました。
それではまた次回の解説記事でお会いしましょう。勉強頑張ってください!応援しています。さようなら!!