はい、どうも中小企業診断士のたかぴーです!
今回はゲーム理論について解説していきたいと思います。
ゲーム理論では複数の専門用語を覚える必要があり、正確に覚えておかないと本試験で足元をすくわれます。
この記事ではそれぞれの用語の違いを事例とともに説明していますので、この機会に是非覚えていただければと思います。
▼YouTube動画でも解説中!
ゲーム理論とは?
ゲーム理論とは、互いに影響を与え合うプレイヤー同士の意思決定に関する理論です。
端的に言うと、意思決定に関する理論だと理解していただければと思います。
主に非協力ゲーム理論と協力ゲーム理論の二つにの理論に大別できますが、中小企業診断士試験で出題されるのは非協力ゲーム理論が多いので、今回はこちらに焦点を絞って解説していきたいと思います。
上の文章を読んだだけだとゲーム理論についてイメージがわかないと思うので、事例に基づいて内容を確認していきます。
まずプレーヤーとしてA社とB社の2つの会社があるケースを考えてみます。
この会社がこれからの会社の戦略を検討していて、お互いが戦略として高価格戦略向かっていくか、それとも低価格戦略に向かっていくかの二択をを考えているとします。
また、お互いがお互いにどちらかの戦略を検討しているかを知っていて、戦略の意思決定は一度しかできないものとします。
そして選択した戦略に応じて利得が決まります。ここでの利得は企業の利益と考えていただいて結構です。

A社が高価格戦略を打ち出して、かつB社も高価格戦略を打ち出した場合は利得が10あります。
一方で、Aが高価格、B社が低価格を打ち出した場合、A社が得る利得は5となります。
このように、A社とB社が打ち出す戦略に応じて、利得が決まっていくことを考えていきます。
Aが低価格を打ち出した場合も、B社の戦略に応じて利得がこのような形で決まり、B社についても同じように自社の戦略とA社の戦略に応じて、自身の利得が決まります。
このような条件のとき、A社とB社はそれぞれどのような戦略を打ち出していくともっとも合理的な経営判断になるのでしょうか?
このように企業の意思決定プロセスをモデル化して考えていくのが、ゲーム理論の一つとなります。
A社とB社の意思決定を考えるには、この図は考えにくいので、もう少しシンプルにしてみましょう。
支配戦略とは?
先ほどの条件を以下のような表でまとめてみました。
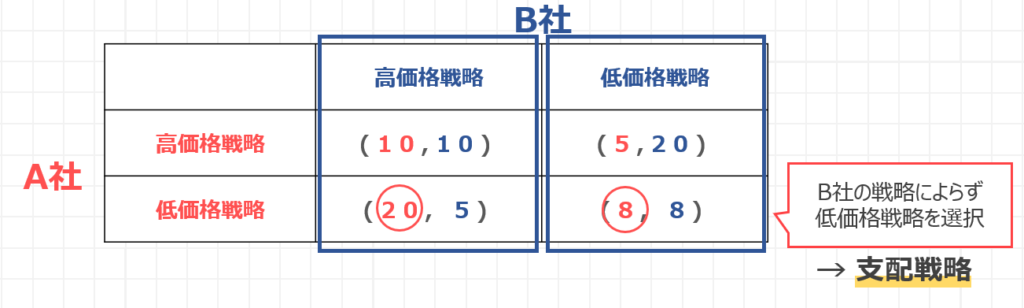
A社B社について、それぞれ高価格戦略と戦略低価格戦略があり、A社の利得は表左側の赤の数値で示されて、B社の利得は表右側の青の数値で示されています。
例えば、A社が低価格、B社が高価格を打ち出した場合、A社の利得は20、B社の利得は5というように表を読み取ります。
それでは、この表を使ってA社とB社はどのように意思決定をしていくか考えていきましょう。
まずA社について考えていきます。
A社は相手の取りうる戦略を知っていますので、当然B社がどのような戦略を打ち出してくるかに応じて、自社の打ち出す戦略を決定します。
もし仮にB社が高価格戦略を打ち出してきたとすると、A社も高価格戦略の場合で利得は10,低価格の時は20となりますので、B社が高価格を打ち出してきた場合は、A社は低価格を打ち出しての利得の20を獲得するのが合理的な判断となります。
一方、B社が低価格を選択した場合は、A社が高価格を選択した場合の利得が5、低価格の場合は8ですので、この場合であっても、A社は低価格戦略を打ち出すことが合理的であると考えることができます。
結果として、A社はB社の戦略によらず、低価格戦略を選択した方が利得が高くなると考えることができます。
このように相手が打ち出す戦略によらず、自身の戦略が一つに決まる戦略を「支配戦略」と言います。
この場合、A社の支配戦略は低価格戦略であるということができますね。
続いてB社についても同じように考えてみましょう。

B社も同じようにAが高価格を打ち出してくるか、低価格を打ち出してくるかによって、自社の戦略を決めていきます。
A社が高価格を打ち出してきた場合、B社も高価格を打ち出すと、青色の利得で、利得は10、B社が低価格だと利得は20となりますので、B社は低価格戦略を打ち出すことが合理的であると考えられます。
今度はA社が低価格を打ち出してきた場合についても考えてみますと、B社が高価格だと利得は5,低価格だと利得は8となりますので、A社が高価格を打ち出した場合でも、B社は低価格戦略を打ち出した方が良いという判断になりますね。
つまりB社についても、A社の戦略によらず低価格戦略を選択した方が合理的であると考えることができます。
これも先ほど同じように、低価格戦略はB社にとっての支配戦略であると言えますね。
ここまでA社とB社の意思決定を考えてきましたが、どうやら両社ともに低価格戦略を打ち出すことが合理的な意思決定だと言えそうですね。
ナッシュ均衡とは?
それではゲーム理論について皆さんの理解が深まったところで、ナッシュ均衡という考え方についてご説明したいと思います。
先ほどまでの説明で、A社B社ともに低価格戦略がそれぞれの支配戦略であるということが確認できました。

お互いが低価格戦略を取り合っている表右下の黄色で囲っている領域については、両社が最適な戦略を取り合っている状態であると言うことができます。
このような状態のことをナッシュ均衡と呼びます。
実際に問題を解く時に、先ほどご紹介した手順に通りに表を読み取って、表の両方に丸が付いた箇所がナッシュ均衡であると考えていただければと思います。
囚人のジレンマとは?
続いて囚人のジレンマについてご説明します。
表の右下がの領域がお互い最適な選択をした場合のナッシュ均衡であるとお話ししましたが、表の左上の部分に着目していただきますと、両社の利得が(10,10)となっていて、ナッシュ均衡の(8,8)よりも両社の利得が増えていることがわかるかと思います。

お互いが最適な選択をしているにもかかわらず、利得をさらに増やす余地がある状態のことを、囚人のジレンマと呼ぶわけですね。
本来であれば、お互いが相談して高価格戦略を両社とも打ち出すことで、両者の利得はナッシュ均衡より増加するはずなのですが、今回考えている非協力的なゲームの場合は、このように囚人のジレンマが発生してしまうケースがあります。
パレート最適 (パレート効率的) とは?
最後にパレート最適、またはパレート効率的という概念を説明します。
先ほど指摘した表の左上の領域について改めて見てみますと、一方の利益を得ると、もう一方の利得が下がる状態であるということが見て取れるかと思います。

例えば、お互い高価格戦略をとっている状態から、A社だけが低価格戦略をとると、A社の利得は22増えますが、一方でB社の利得が5に減ってしまいます。
同じように、B社だけが低価格戦略をとると、B社の利得は増えますが、逆にA社の利得は減りますね。
このように、一方の利得を上げるには、もう一方の利得を下げる必要がある状態のことを、
パレート最適と呼びます。
反対に、囚人のジレンマのように他の誰かの利得を下げなくても、一方の利得を上げられる状態のことは、パレート非効率といいますので、合わせて覚えておきましょう。
過去問を解いてみよう (平成24年度 第23問)
それではここまでの内容を、過去問を解いて復習してみましょう。
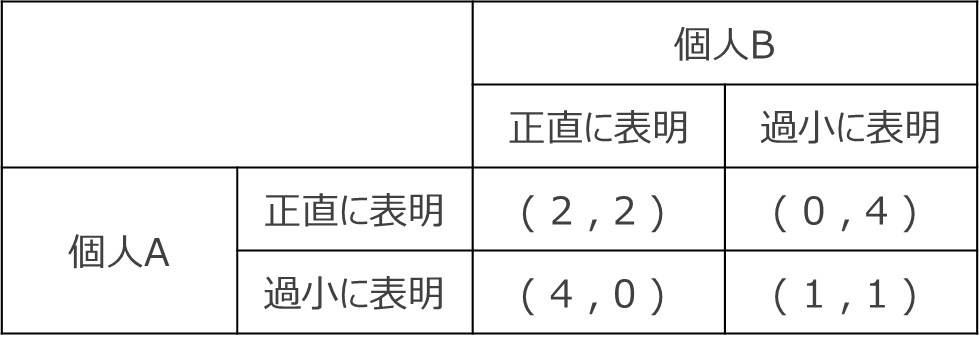
下表は、「囚人のジレンマ」として知られる非協力ゲームの利得表である。いま、2人の個人 (個人Aと個人B) が1度限りの取引を行い、2つの選択肢 (自らの選好を「正直に表明」するか、「過小に表明」する) のいずれかを選択することができる。
なお、以下の表中にあるカッコ内の値は、それぞれ左側が個人Aの利得、右側が個人Bの利得を示している。この表から得られる記述として、最も適切なものを下記の解答群から選べ。ア 個人Aが非協力的に利得の最大化をめざすならば 「過小に表明」 を選択する。
イ 個人Aにとって 「正直に表明」 を選択するのが支配戦略である。
ウ 個人Aは、個人Bの選択に応じて最適な行動を変化させる。
エ 個人Bが 「正直に表明」 を選択してくれることが確実であれば、個人Aも 「正直に表明」を選択することが合理的である。
中小企業診断士試験 財務会計 平成24年度 第23問
文章を読むと、個人Aと個人Bが「正直に表明」するか、「過小に表明」するかのいずれかを選択することができて、表の左側に個人Aの利得、右側に個人Bの利得が示されていることがわかりますね。
先ほどまでの解説と同じように、個人AとBがどのように意思決定をするか考えていきましょう。
まず個人Aについて考えてみます。
個人Aは個人Bの選択に応じて自身の選択を決めますので、まず個人Bが「正直に表明」したケースを考えてみますと、個人Aが「正直に表明」すると利得は2、「過小に表明」すると利得は4になりますので、個人Aは「過小に表明」した方が良いということになります。
また、個人Bが「過小に表明」したことを考えてみますと、個人Aが「正直に表明」すると利得は0、「過小に証明」すると利得は1となりますので、この場合でも個人Aは「過小に表明」した方が良いとなります。
続いて個人Bの意思決定についても考えてみます。
個人Aが「正直に表明」してきたと考えると、個人Bは「正直に表明」すると利得は2、「過小に表明」すると利得は4となりますので、個人Bは「過小に表明」した方が良いということになります。
また、個人Aが「過小に表明」してきた場合を考えてみると、個人Bが「正直に表現」したときの利得は0、「過小に表明」すると利得は1になりますので、この場合も、個人Bは「過小に表明」した方が良いということになります。
ゲーム理論の問題では、このような表が与えられてきたときは、まずは今の手順で表に丸印をつけて、どのように意思決定をするかを考えてみてから各選択肢を検討していくと良いでしょう。
それでは選択肢を見てきます。
✅選択肢ア
個人Aが非協力的に利得の最大化を目指すならば、「過小に表明」を選択する。
この選択肢は正解となりますね。
個人Aが自身の利益の最大化を目指して意思決定をした結果、個人Bの選択によらず、「過小にに表明」するを選択していることが、表から読み取れます。
いきなり正解が出てきてしまいましたが、他の選択肢についても、念のため検討していきましょう。
✅選択肢イ
個人Aにとって「正直に表明」を選択するのが支配戦略である。
これは誤りですね。個人Aの支配戦略は「過小に表明」することです。
✅選択肢ウ
個人Aは個人Bの選択に応じて最適な行動を変化させる。
これも誤りですね。個人Aは個人Bの選択によらず、常に「過小に表明」することで、利得を最大化できるのでした。
✅選択肢エ
個人Bが「正直に表明」を選択してくれることが確実であれば、個人Aも「正直に表明」することが合理的である。
実際に表を見てみますと、個人Bが「正直に表明」したとき、個人Aが「正直に表明」した時の利得は2、「過小に表明」すると利得は4となりますので、やはり「過小に表明」した方が合理的となりますので、「正直に表明」することが合理的であるという選択表現は誤りとなります。
ちなみにこの問題には書かれていませんが、個人AとBがお互いに「過小に表明」しているという表の右下がナッシュ均衡、お互いが「正直に表明」するとした表の左上の部分がパレード最適となります。
ナッシュ均衡とパレート最適が異なる位置にありますので、このケースでも囚人のジレンマが発生しているということが読み取れますね。
まとめ
最後にまとめです。
- 支配戦略
相手の戦略に関係なく決まる自身の戦略のこと - ナッシュ均衡
各プレイヤーが最適な戦略を取り合っている状態のこと - 囚人のジレンマ
ナッシュ均衡の組み合わせよりも全プレイヤーの利得合計を更に大きくできる余地がある状態のこと - パレート最適 (パレート効率的)
他の誰かの利得を下げない限り、どのプレイヤーの利得を上げることができない状態のこと
支配戦略とは相手の戦略に関係なく決まる自身の戦略のことを言いました。
相手の戦略によって自分の戦略が決まる場合は支配戦略とはならない点にご注意ください。
続いて、ナッシュ均衡とは各プレイヤーが最適な戦略を取り合っている状態のことを指します。
ナッシュ均衡は常に1つだけあるわけではなく、2つがあるケースもありますので、問題の選択肢によって、騙されないように注意してください。
続いて囚人のジレンマは、ナッシュ均衡の組み合わせよりも全プレイヤーの利得合計をさらに大きくできる余地がある状態のことを言います。
最後にパレート最適は、他の誰かの利得を下げない限り、どのプレイヤーの利得も上げることができない状態のことを言います。
今回の確認した過去問では、支配戦略以外のの用語は出てきませんでしたが、実際に出題実績がありますので、是非ご自身で過去問を解いて、確認いただければと思います。
それでは今回の解説記事はここまでとしたいと思います。
ここまでご覧いただき、ありがとうございました。
それではまた次回の解説記事でお会いしましょう。勉強頑張ってください!応援しています。さようなら!!