はいどうも、中小企業診断士のたかぴーです。
今回はLM曲線をテーマに解説していきたいと思います。
前回までにIS曲線などの財市場に関する内容を扱ってきましたが、今回は貨幣市場に着目して、利子率と国民所得の関係を描いたLM曲線を取り上げたいと思います。
このLM曲線は、診断士試験でも頻出論点ですし、次に続くIS-LM分析を理解する上でもぜひ理解しておきたいところです。
グラフで図解しながら丁寧に解説しますので、ぜひこの機会にマスターしておきましょう。
財市場と貨幣市場
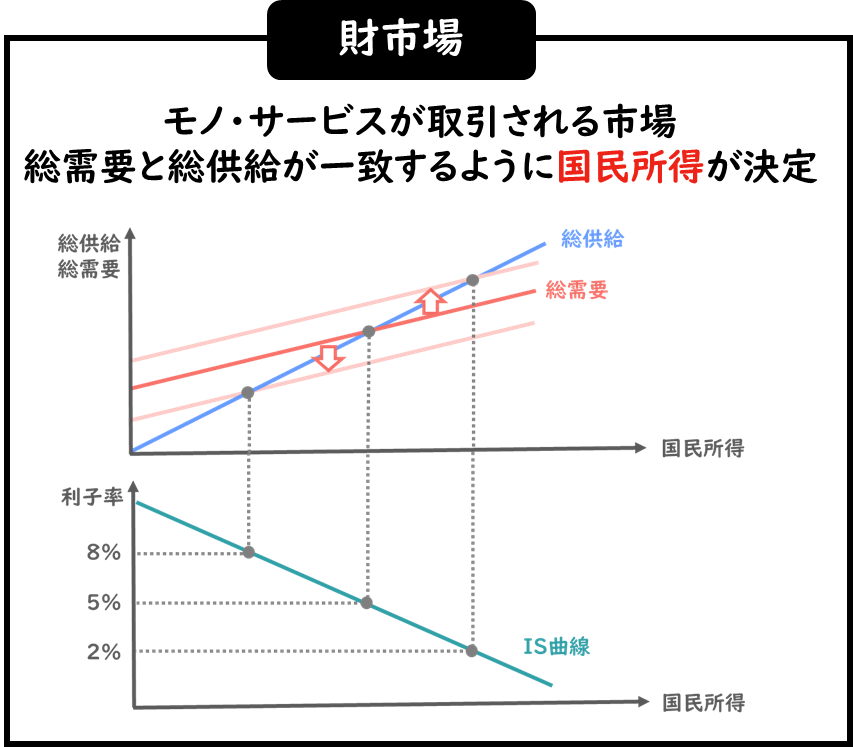
前回までは、以下のようなグラフを使いながら、総需要と総供給の関係や、国民所得と利子率の関係からIS曲線を見てきました。
ここで見てきたのは、いわゆる財市場と言われる市場で、モノやサービスの取引が行われる市場です。
ここでは、総需要と総供給が一致するように、国民所得が決定していました。

一方、今回のテーマであるLM曲線は、貨幣市場を見ていきます。
貨幣市場では、「貨幣=お金」の需要と供給の関係から、利子率がどのように決まるかを分析します。
LM曲線は、この貨幣市場の均衡した状態における、利子率と国民所得の組み合わせを表す曲線となります。
ここでは、IS曲線とLM曲線では、見ている市場が異なるんだという、何となくのイメージを持っていただければ十分です。
ここからは貨幣市場について、さらに詳しく見ていきましょう。
貨幣供給曲線とは?
まずは、貨幣供給曲線について確認してみます。
貨幣供給曲線とは、貨幣の供給量と利子率の関係を表したグラフです。
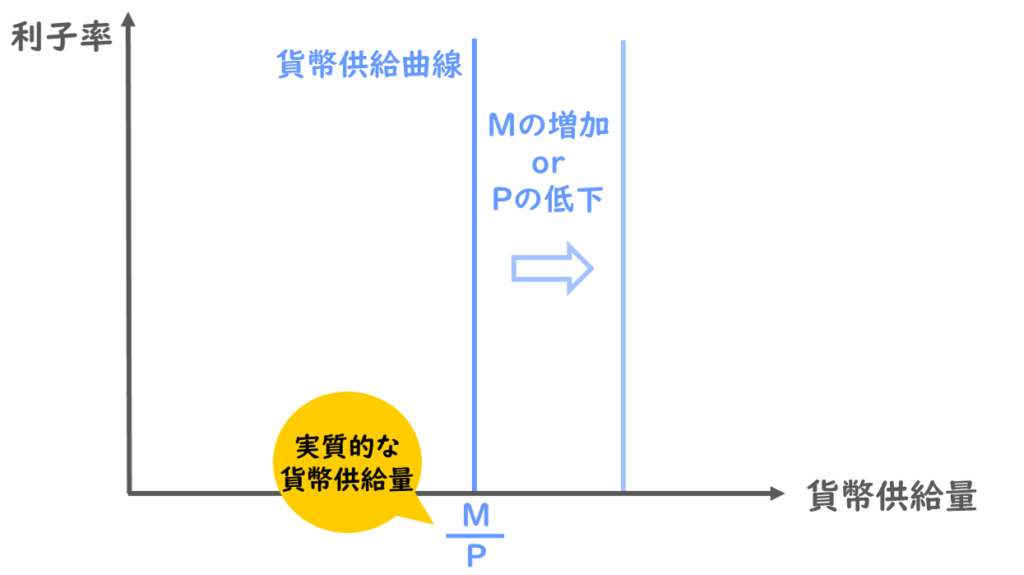
横軸に貨幣供給量・縦軸に利子率を取ると、貨幣供給曲線は以下のような垂直な直線として描かれます。
ここで用語解説です。
今、貨幣供給量はM/Pと表していますが、ここでいうMはマネーサプライのことで、世の中に出回っているお金の量を表しています。
一方で、Pは物価のことで、モノ・サービスの平均的な値段を指しています。
貨幣供給量をM/Pで表しているということは、マネーサプライを物価水準で割り返すことで、実質的な貨幣供給量を表しているということになるわけですね。
貨幣需要曲線を見てみると、傾きが0、つまり垂直な直線ですので、利子率とは全く関係なく貨幣供給量が決まることが読み取れます。
そして、分子であるマネーサプライが増加するか、分母である物価水準が低下すれば、実質的な貨幣供給量が増えますので、貨幣供給曲線は以下のように右方向にシフトします。
中央銀行による貨幣供給については、また別の機会で解説しますが、貨幣供給曲線が垂直であることと、曲線のシフト要因は、そう難しいものではないと思いますので、ここでは結論だけ押さえるようにしてください。
貨幣の投機的需要
次に、貨幣需要曲線です。
貨幣需要は、大きく分けて2つの要因によって決まります。
1つ目は投機的需要で、利子率が下がれば貨幣需要は増えると考えます。
最近は新NISA制度も始まって投資をされる方も増えてきましたが、ここでは投資対象としての債券について考えます。
債券の利子率が高い時は、多くの方はたくさんの債権を買って利息で儲けたいと考えます。
債券を買うと現金を手放すことになりますので、現金割合は減少しますね。
一方で、債券の利子率が低いと儲かりませんし、いざというときに換金しづらいので、現金で持っておこうという気持ちが強くなり、貨幣の需要は増えるわけですね。
ですので、横軸に貨幣需要を、縦軸に利子率を取ると、貨幣需要曲線はこのように右肩下がりの直線として描くことができます。

先ほど確認したように、利子率が下がれば、貨幣需要は増えるという関係となっていますね。
このように、貨幣需要を債権と貨幣の所有割合という投資的な観点から説明するアプローチを、貨幣の投機的需要といいます。
貨幣の取引需要
続いて、貨幣の取引需要です。
これは日々の買い物や企業の仕入れなど、経済活動の中で必要になるお金の需要です。
国民所得が増えると、この貨幣の取引需要は増加します。
たとえば所得が増えれば、その分消費・取引量も増えるため、より多くのお金を手元に持っておきたいというニーズが出てくるわけですね。
先ほどは貨幣の投機的需要によって、貨幣需要曲線が右肩下がりになると説明しました。
例えば今、利子率2%で、国内の貨幣需要が2兆円あったとしましょう。
ここでさらに、国民所得が増えると、貨幣の取引需要によって、同じ利子率2%でも、貨幣需要は4兆円にまで増加します。
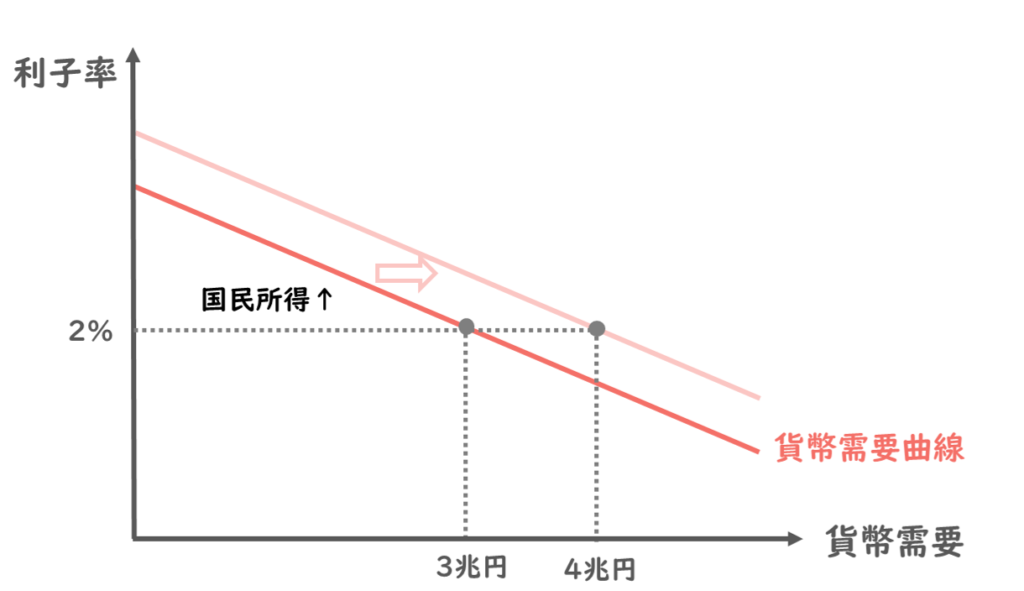
つまり国民所得が増えると、貨幣需要曲線はこのように右方向にシフトするわけですね。
ここまで見てきたように、貨幣需要曲線は利子率に応じて変化する投機的需要と、国民所得に応じて変化する取引需要の2つの要因によって決定するということがわかりました。
以上の内容がわかると、LM曲線について理解できるようになります。
LM曲線の導出過程
それでは、いよいよ本題であるLM曲線の導出について見ていきましょう。
LM曲線とは、貨幣市場が均衡する際の、国民所得と利子率の関係を表す曲線のことを言います。
まずは前半の貨幣市場が均衡している状態を確認してみます。
横軸に貨幣需要と貨幣供給を、縦軸に利子率を取ると、まず貨幣需要曲線は、以下の赤色ような右肩下がりの直線となるのでした。
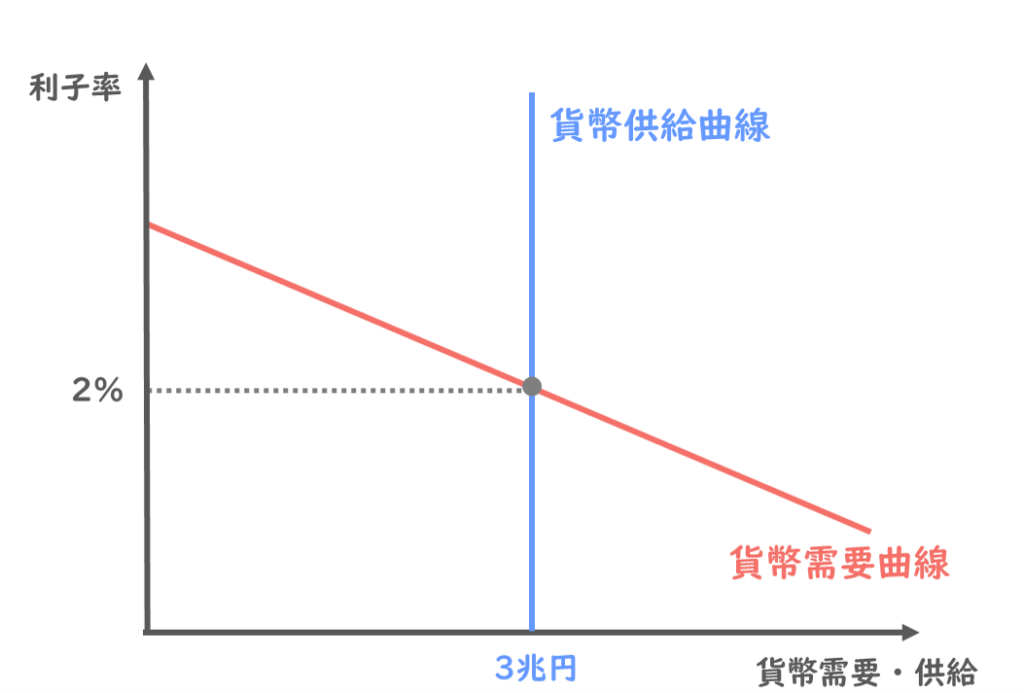
そして、貨幣供給曲線は、上の青色のような垂直の直線として描けるのでしたね。
貨幣市場が均衡状態にあるということは、この貨幣の需要と供給が一致していることを指します。
例えば今、利子率2%、貨幣需要・貨幣供給ともに3兆円で均衡していたとしましょう。
LM曲線は、このときの利子率と国民所得の関係を考えます。
縦軸に利子率を、横軸に国民所得を取ると、貨幣市場が均衡している利子率2%のときの国民所得は10兆円だったとします。
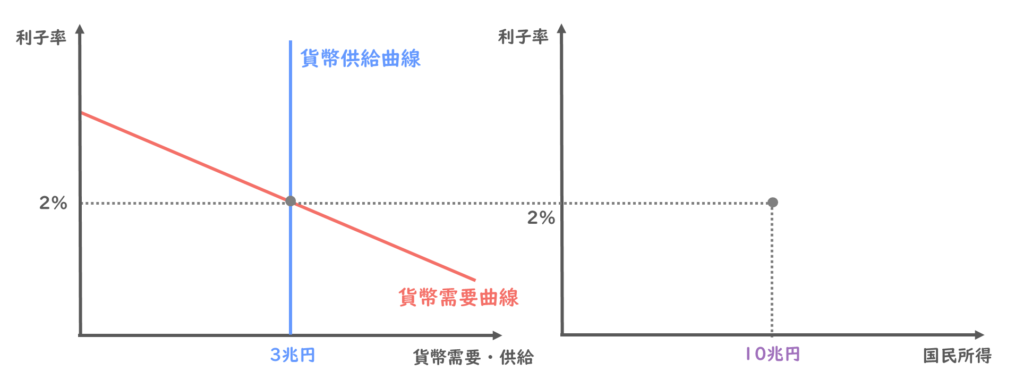
ここで、国民所得が15兆円にまで増加した時のことを考えてみます。
国民所得が増加すると、貨幣の取引需要が増えるので、貨幣需要曲線は右方向にシフトするのでしたね。
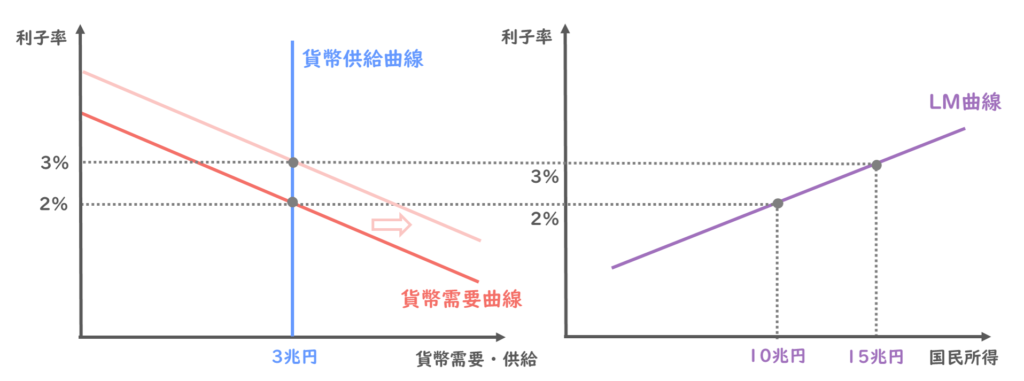
今考えたいのは、貨幣市場の均衡点ですので、新しい貨幣需要曲線と供給曲線の交点は3兆円で変わらず、利子率だけが3%に上がることが読み取れます。
そうすると、国民所得が15兆円に上がった時に、貨幣市場が均衡する利子率は3%ということになりますので、国民所得と利子率の関係は以下の点で表すことができますね。

以上のように、利子率と国民所得の組み合わせを点としてグラフ上にプロットして、点を線で繋ぐと、LM曲線を描くことができます。
LM曲線は、右肩上がりの直線として描かれるわけですね。
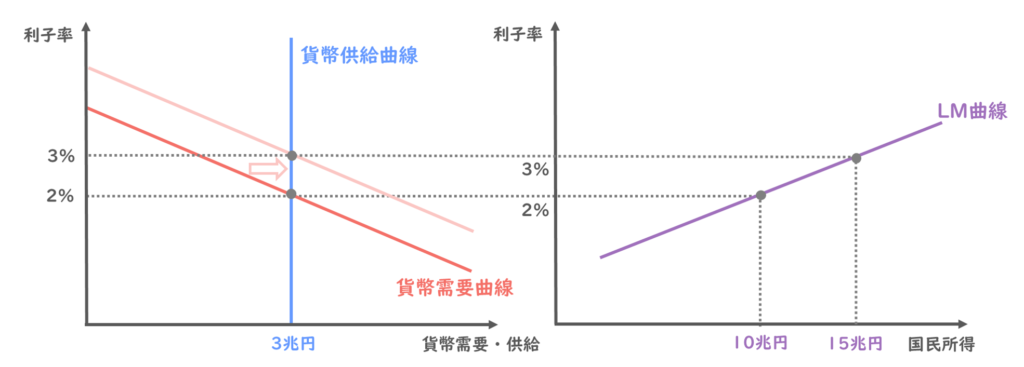
LM曲線の導出過程も、IS曲線と同様、ぜひご自身で作図をしながら確認していただきたい内容です。
この導出をご自身でできるようになれば、このIS-LM分析の応用問題へも対応しやすくなるかと思います。
実質貨幣供給量とLM曲線の関係
続いて、LM曲線のシフトと傾きについて見ていきたいと思います。
まず、LM曲線のシフト要因についてです。
実質貨幣供給量が増えると、LM曲線は右方向にシフトします。
例えば今、貨幣市場とLM曲線が以下のように描けていたとしましょう。

先ほど説明したように、貨幣供給量が増加すると、貨幣供給曲線は右方向にシフトするのでしたね。
そうすると、貨幣需要曲線との交点は利子率2%、貨幣需要・供給は4兆円となりました。
ここでのポイントは、貨幣供給量は変化しましたが、国民所得は変わらないことです。
ですので、国民所得10兆円のときの利子率は、貨幣市場の均衡点が変化したことで、2%になります。
また、国民所得が15兆円に増え、取引需要増加によって貨幣需要曲線が右方向にシフトした時も、貨幣市場の均衡点は変わります。
利子率は2%、貨幣需要・供給は4兆円となりますね。
ですので、国民所得15兆円のときの利子率は4%となるわけですね。
以上の点を線で結ぶと、新しいLM曲線は右方向にシフトしていることが読み取れます。
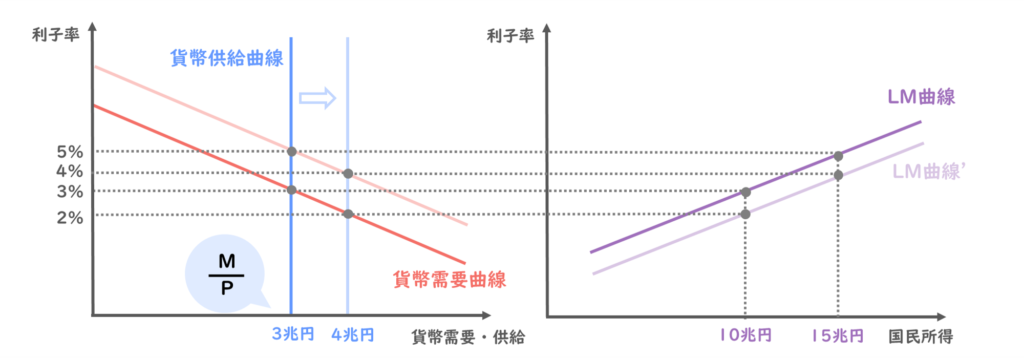
ここまでの内容をまとめてみます。
実質貨幣供給量が増えると、貨幣均衡点の利子率が下がり、同じ国民所得でも利子率が低くくなるため、LM曲線は右方向にシフトする、ということになります。
最低でも、赤字で書いた結論だけ覚えていただければと思いますが、こちらもプロセスをご自身で説明できるようにしていただきたいところです。
なお、実質貨幣供給量はM/Pで表されるのでした。
つまり、名目貨幣供給量であるマネーサプライの増加か、物価水準の低下が起これば、貨幣供給量が右方向にシフトすることになります。
特に分母側の物価水準の影響を受ける点については、忘れやすい観点ですので、お気を付けください。
貨幣需要の所得弾力性とLM曲線の関係
次に、LM曲線の傾きについてです。
LM曲線の傾きは、貨幣需要の所得弾力性に影響されます。
貨幣の所得弾力性とは、所得の変化に対する貨幣需要の変化量のことですね。
例えば今、貨幣市場とLM曲線が以下のように描けていたとしましょう。

貨幣需要の所得弾力性が大きいということは、同じ国民所得の増加に対して、貨幣需要は大きく増加することを意味しますので、国民所得が10兆円から15兆円に増加すると、貨幣需要曲線は以下のオレンジの直線のように、大きく右方向にシフトするということになります。
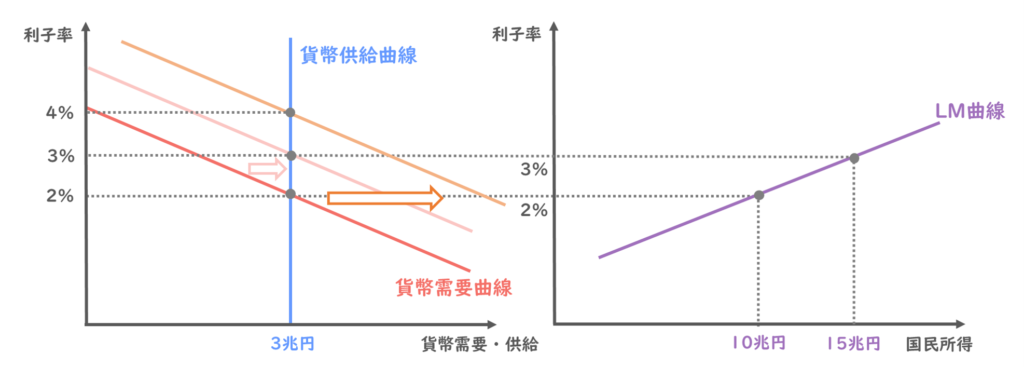
新しい貨幣均衡点は利子率4%となりましたので、国民所得15兆円のときの利子率は4%ということになりますね。
国民所得10兆円のときの利子率は2%のままで変わりませんので、この2つの点を結ぶと、新しいLM曲線は以下のように描くことができます。
前のLM曲線と比較すると、傾きが急になったことが読み取れます。
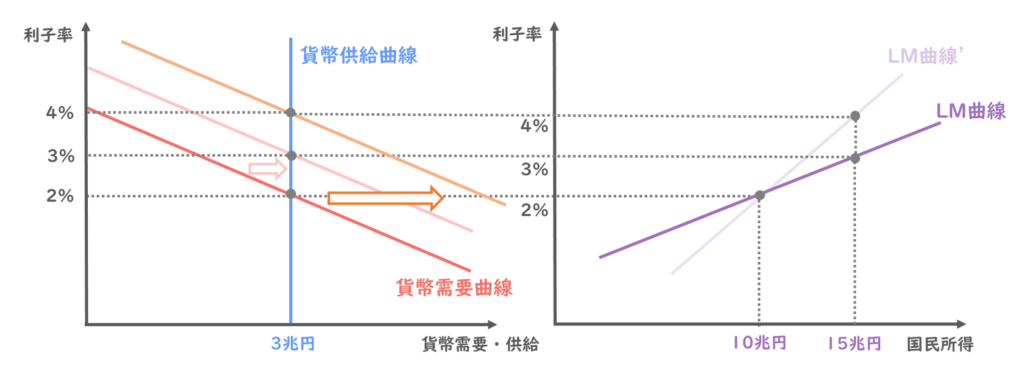
ここまでの内容をまとめてみます。
貨幣需要の所得弾力性が大きいと、所得増加に対して貨幣需要曲線は大きく右方向にシフトします。
貨幣均衡点の利子率の増加を招くので、LM曲線の傾きは急になる、ということになります。
貨幣市場の均衡とLM曲線の関係がわかっていれば、そこまで難しいものでものないので、こちらも理屈を理解するように努めていただければと思います。
貨幣需要の利子率弾力性とLM曲線の関係
最後は貨幣需要の利子率弾力性です。
ここが今回解説する内容で、最も難しい論点です。
まず、貨幣需要の利子率弾力性とは、利子率の変化に対する、貨幣需要の変化量を表します。
例えば今、貨幣市場とLM曲線が以下のように描けていたとします。

貨幣需要の利子率弾力性が大きいということは、利子率が少し下がっただけで、貨幣需要は大きく増えることを意味しますので、もともと利子率が2%から1%に下がった時は4兆円にまでしか増えなかった貨幣需要が、6兆円にまで増えるイメージとなりますね。
そうすると、貨幣需要曲線の傾きは、以下のように緩やかになります。
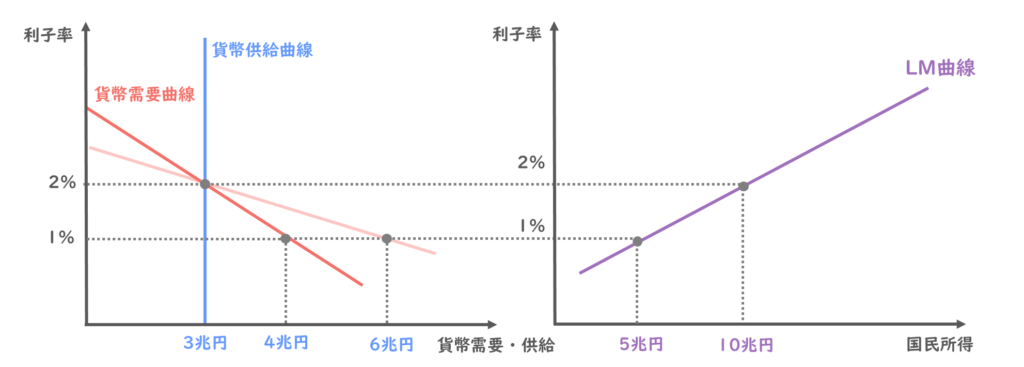
先ほどの所得弾力性は、所得の変化に対する貨幣需要の変化を考えたので、貨幣需要曲線はシフト、今回は利子率の変化に対する貨幣需要の変化を考えているので、貨幣需要曲線の傾きが変わることがポイントです。
貨幣の投機的需要と、取引需要のどちらに影響する内容かを判断できるようにしましょう。
さて、ここからはLM曲線への影響を見ていきたいと思います。
貨幣需要曲線の傾きが変わった状態で、国民所得が10兆円から15兆円に増加した時のことを考えてみます。
国民所得が増えたので、貨幣需要は取引需要の増加に伴い、右方向にシフトし、同じ利子率であれば5兆円にまで増加する圧力が加わります。
ただし、貨幣市場はあくまで需要と供給が一致する点で決まりますので、もともとの均衡点である3兆円になるように、利子率を引き上げます。
利子率弾力性が大きくないときは、3%にまで利子率を引き上げると均衡点に落ち着くのでしたね。
ですが、今は利子率弾力性が大きいケースを考えています。
貨幣需要の利子率弾力性が大きいと、利子率が下がれば貨幣需要は大きく増えますが、逆に利子率が上がれば、貨幣需要は大きく減ることになります。
ですので、もともとの均衡点である3兆円になるようにするには、利子率をそこまで引き上げなくてもよいと考えられます。
結果的に、均衡点における利子率は2.5%となり、国民所得が15兆円のときの利子率も2.5%となります。
もともとの点と合わせて線で結ぶと、新しいLM曲線は以下のように描けますね。
前のLM曲線と比較すると、傾きが緩やかになったことが読み取れます。
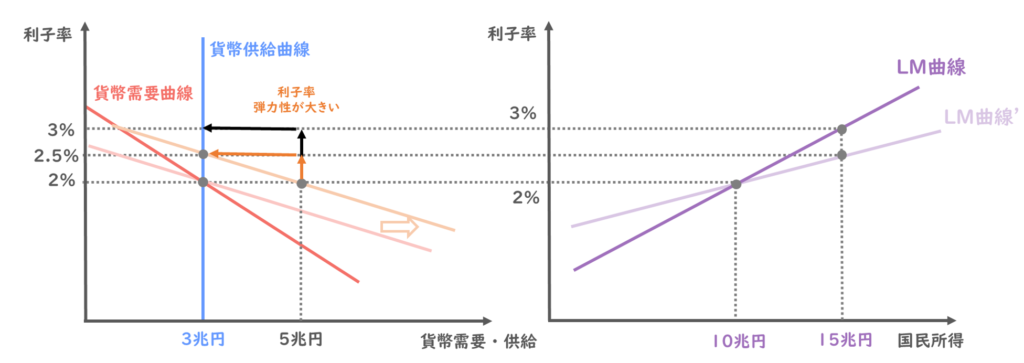
ここまでの内容をまとめます。
貨幣需要の利子率弾力性が大きいと、貨幣需要曲線は緩やかになります。
この時、国民所得が増え、貨幣需要曲線が右シフトする時、貨幣需給を均衡させるための利子率の増加分は少なくて済むので、LM曲線の傾きは緩やかになる、ということになります。
このプロセスを正確に理解して、試験本番で再現するのは難易度が高いので、ここは結論の丸暗記で済ませてよいかと思います。
もちろん、理解できることに越したことはないので、余裕のある方はチャレンジしてみてください。
過去問を解いてみよう
それではここまでの内容を、過去問を解いて復習してみましょう。
LM曲線に関する記述として、最も適切なものはどれか。
ア 貨幣需要の所得感応度が大きいほど、LM曲線の傾きはより緩やかになる。
イ 貨幣需要の利子感応度が大きいほど、LM曲線の傾きはより緩やかになる。
ウ 資産効果に伴う貨幣需要の増加は、LM曲線を右方にシフトさせる。
エ 投資の利子感応度が大きいほど、LM曲線の傾きはより緩やかになる。
オ 名目貨幣供給の増加は、LM曲線を左方にシフトさせる。
LM曲線に関して、正しいものを選ぶ問題ですね。
選択肢をひとつずつ見ていきましょう。
✅選択肢ア
所得弾力性が大きいと、LM曲線の傾きは急になるので、誤りですね。
✅選択肢イ
これは正しいですね。
感応度と弾力性は同じ内容を示していますので、惑わされないよういに注意しましょう。
✅選択肢ウ
これは今回解説した内容に含まれないので、保留にしたい選択肢ですね。
✅選択肢エ
投資の利子率弾力性が大きくても、LM曲線には影響がありません。
前回学習した通り、IS曲線の傾きは緩やかになりますが、いずれにしても選択肢エは誤りとなります。
✅選択肢オ
貨幣供給が増加すると、貨幣供給曲線は右方向にシフトし、LM曲線も右方向にシフトするので誤りです。
以上から、選択肢イがこの問題の正解となりますね。
LM曲線が影響を受ける内容を確認する問題でしたが、万が一、ド忘れしてしまったときに備えて、ご自身でグラフを描きながら正誤判定できるようにすることがベストです。
この問題を自信を持って回答できる頃には、IS-LM分析も難なく理解できるようになると思いますので、ぜひ、繰り返し解いて理解を深まていただければと思います。
なお、選択肢ウの内容は難しく、今回は解説をスキップしますので、興味がある方だけ、ご自身で調べてみてください。
まとめ
それでは最後にまとめです。
今回はLM曲線に関して学習をしました。
LM曲線とは、貨幣市場が均衡する際の、国民所得と利子率の関係を表す曲線なのでしたね。
横軸に国民所得、縦軸に利子率をとると、以下のような右肩上がりの直線として表すことができました。
そして、各種条件に対してLM曲線の変化するのでした。
実質貨幣供給が増加すれば、LM曲線は右方向にシフト、貨幣需要の所得弾力性が大きいと傾きが急に、貨幣需要の利子率弾力性が大きくと傾きは緩やかになるのでした。
この辺はなぜそうなるのかということを、ご自身でグラフを描きながら説明できることが理想的です。
そうすることで丸暗記に頼らず、どのような応用論点が来ても対応できるようになるかと思います。
はい、というわけで、今回はLM曲線について解説してみました。
ここまで解説してきた様々な論点がちゃんと理解できていることが前提となりますので、
解説していても、皆さんがきちんと付いてこられているか、正直不安です。
付いてこられなかった方は、そもそも難しい内容を学ぼうとしていると自覚した上で、
過去のIS曲線の記事などにも戻りながら、理解を深めていただければと思います。

次回はいよいよ、IS-LM分析となりますので、楽しみにお待ちください。