はいどうも、中小企業診断士のたかぴーです。
今回はIS曲線をテーマに解説していきたいと思います。
前回の記事では、均衡国民所得について確認しましたが、今回はその発展として、マクロ経済学におけるIS曲線の考え方を扱います。
IS曲線は、財市場の均衡を表す曲線で、後に登場するLM曲線とセットで経済の均衡を捉える重要なフレームワークとなります。
グラフと合わせて押さえることで、理解しやすくなりますので、ぜひ最後までご覧ください。
均衡国民所得とは?
まずは前回までの復習です。
前回まで学習した均衡国民所得とは、総供給と総需要が一致するときの国民所得なのでしたね。
横軸に国民所得、縦軸に総供給と総需要をとってグラフで表してみると、総需要と総供給曲線は以下のように表されました。

そして需要と供給が一致するポイントで国民所得が決定するのでしたね。
IS-LM分析ではこの国民所得の考え方が全てのベースとなるので、不安な方は以下の解説記事からから確認してみてください。

IS曲線とは?
それでは本題のIS曲線です。
IS曲線とは、国民所得と利子率の関係を表す曲線のことをいいます。
横軸に国民所得を取り、今度は縦軸に利子率を取ります。
そして利子率と国民所得の関係は、以下のような右肩下がりの直線として表すことができます。

これをIS曲線と呼ぶわけですね。
グラフから、利子率が下がれば国民所得が増加するといった関係が読み取れますね。
ここからは、なぜ利子率が下がれば国民所得が増加するのか、その考え方を確認していきたいと思います。
利子率と投資額の関係
まず、利子率と投資の関係です。
経済学では、基本的に利子率が下がると投資は増えると考えます。
ここでいう投資とは、工場や機械などの設備投資のことですね。
多くの企業は投資を行う場合、銀行から融資を受けて設備を購入しますが、このときの利子率が低ければ低いほど、利息を低く抑えることができますので、投資が活性化すると考えられます。
ですので、横軸に投資額、縦軸に利子率を取ると、この2つの関係は以下のような右肩下がりの直線として表すことができます。

つまり、利子率が下がれば投資が増えるといった関係ですね。
グラフで表すと難しく感じられるかもしれませんが、単純に借金に対するコストが下がれば投資が増えると言っているだけですので、ここはシンプルに理解いただければと思います。
投資と国民所得の関係
続いて、投資と国民所得の関係を確認しておきましょう。
経済学では、投資が増えると国民所得も増えると考えます。
こちらもグラフを描きながら確認してみましょう。
国民所得は総需要と総供給が一致する点で決定するのでしたね。
そして、総需要の計算式を表してみると、以下のような計算式で表すことができるのでした。
総需要 = c (Y ー T) + C0 + I + G
この時、投資のIは、総需要曲線における切片を表していました。
ですので、投資が増えれば総需要曲線は上方向にシフトします。
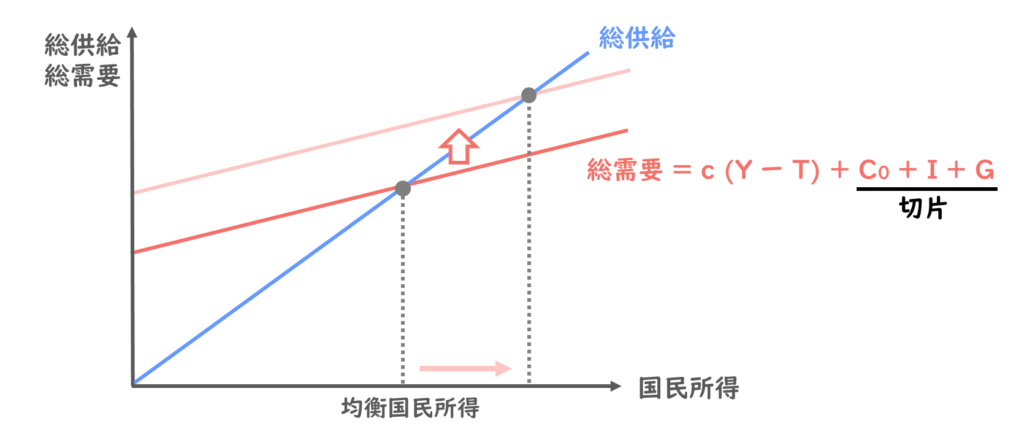
均衡国民所得は総需要と総供給が一致する点ですので、投資が増えて総需要曲線が上方向にシフトすれば、国民所得は増加することが読み取れます。
反対に、投資が減り総需要曲線が下方向にスライドすれば、均衡国民所得は減るわけですね。
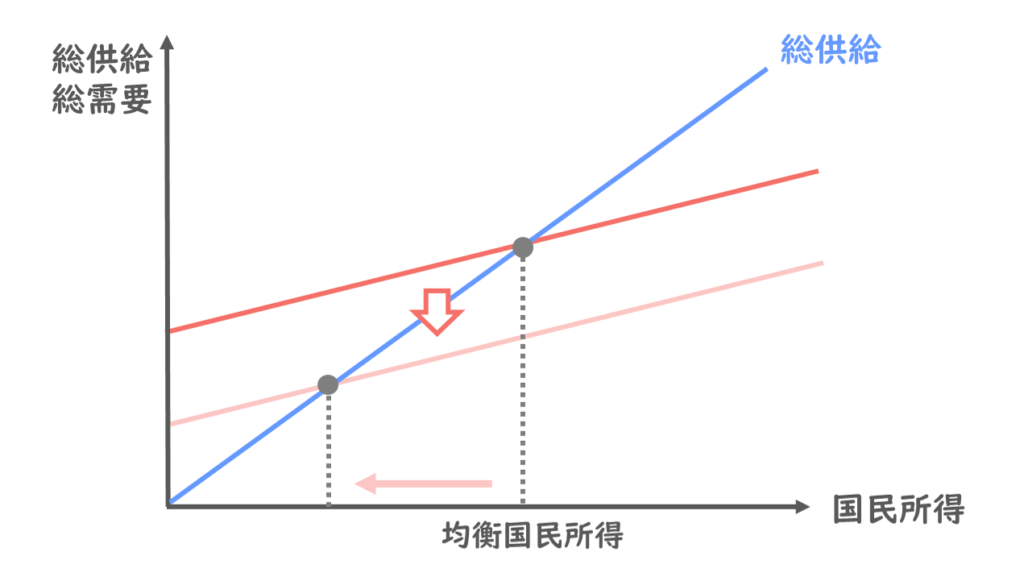
ここでも「投資が増えれば国民所得が増える」というのは、なんとなく直感的にそうだろうなと思うことを、数学的に説明しているだけだと理解いただければと思います。
ただし、切片の値が増減すればグラフが上方向・下方向にシフトするという事は、この後も重要な考え方となりますので、しっかりと押さえていただければと思います。
なぜIS曲線が右肩下がりなのか?
ここまでの内容を踏まえて、IS曲線がどうして右肩下がりになるのか、確認していきましょう。
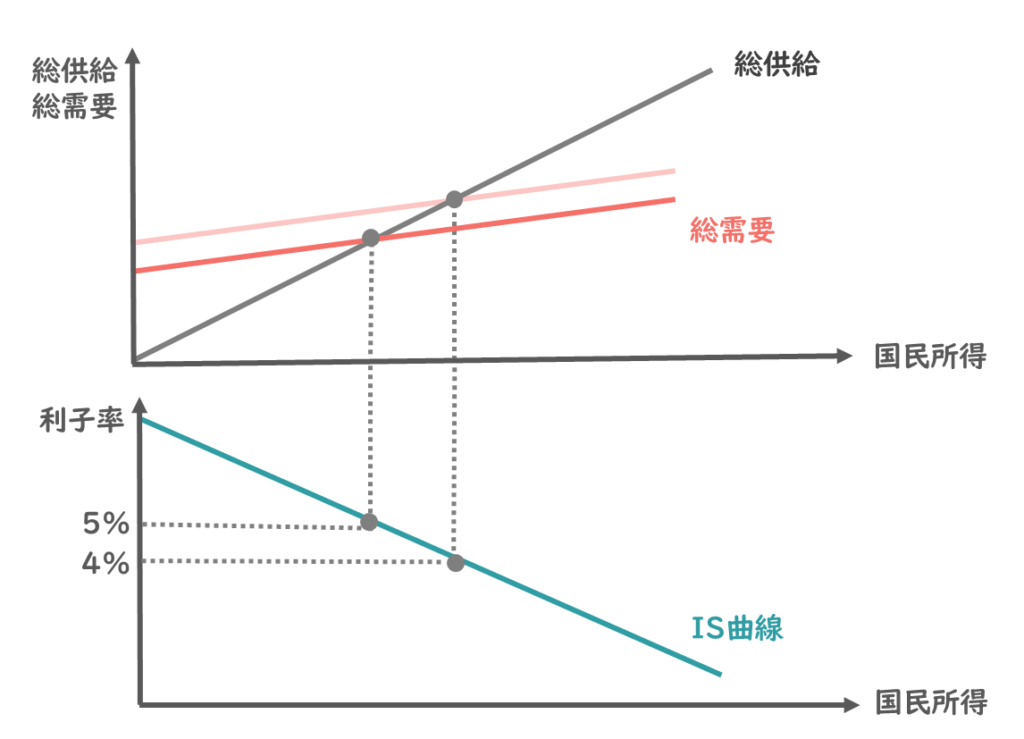
まずは上側に総需要曲線・総供給曲線を描いて、下側には国民所得と利子率の関係を表したグラフを描いていきたいと思います。
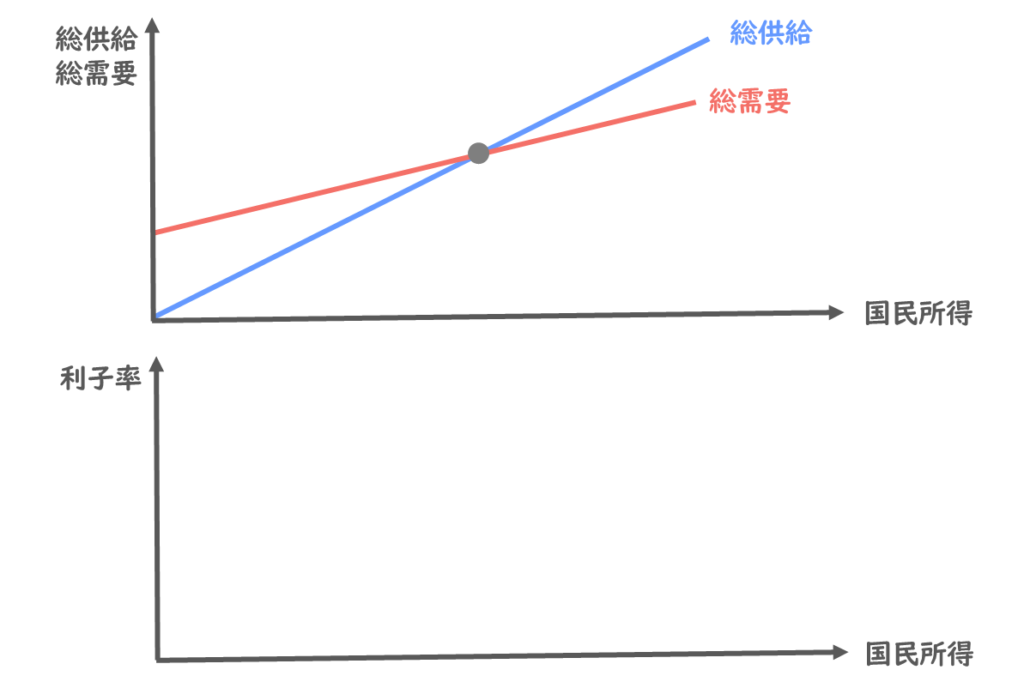
均衡国民所得は総需要と総供給が一致する点で決まります。この時の利子率は5%だったとしましょう。
上下のグラフで、均衡国民所得は一致しますので、利子率5%のときの利子率・国民所得の関係は以下の通りとなります。

ここで、利子率が5%から2%に減少したことを考えてみます。
利子率が下がると、投資額はどうなるのでしたでしょうか?
そうです、利子率が下がると、投資は増えるのでしたね。
そして、投資が増えると総需要曲線は上方向にシフトするので、国民所得は増加することになります。
上下のグラフで均衡国民所得は一致するので、利子率が2%に下がると、国民所得は以下の位置だということになりますね。

さらに、利子率が5%から8%に上がったことを考えてみましょう。
利子率が上がると今度は投資が削減されますので、国民所得は減少してしまいます。
ですので、利子率8%の国民所得は以下の位置ということになるわけですね。

これらの点を線で結ぶと、以下のような右肩下がりの直線として表されます。
これがIS曲線と呼ばれる直線になるわけですね。

ここまで見てきた通り、基本的に利子率が下がると投資は増えます。
投資が増えると国民所得も増えるので、赤で示した通り、利子率が下がると国民所得が増えるという関係が成り立つので、IS曲線は右肩下がりになるわけですね。
ここは結論だけ押さえるというより、なぜIS曲線が右肩下がりになるのかということを、グラフを描きながら、今お見せしたような導出過程をご自身で説明できるようになっていただきたいところです。
そうすることで、この後説明する論点についても理解がしやすくなるかと思いますので、ぜひチャレンジしてみてください。
政府支出とIS曲線の関係
ここからは、IS曲線の特徴について確認してみましょう。
まずは政府支出とIS曲線の関係です。
ここまで確認した通り、総需要曲線は以下のような計算式で表され、独立消費C₀、投資I、政府支出Gは切片として表すことができましたね。
総需要 = c (Y ー T) + C0 + I + G
また、平時のIS曲線は以下のように表されていたとします。
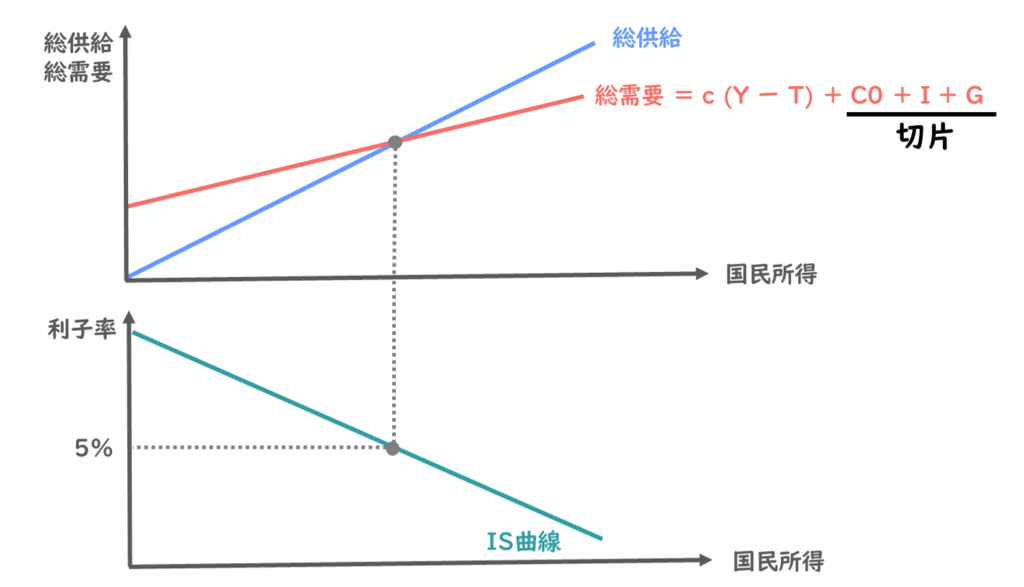
ここで利子率は5%のままで政府支出が増加されたことを考えてみましょう。
政府支出が増加されると、切片の値が増えることになりますので、総需要曲線は上方向にシフトします。
そうすると、国民所得が増加しますね。
この時、利子率は変わらない状態で国民所得が増えていますので、利子率5%の国民所得は、以下の位置に変更されるということになりますね。
ですので、IS曲線は政府支出が増えると、このように全体として右方向にシフトすることになります。
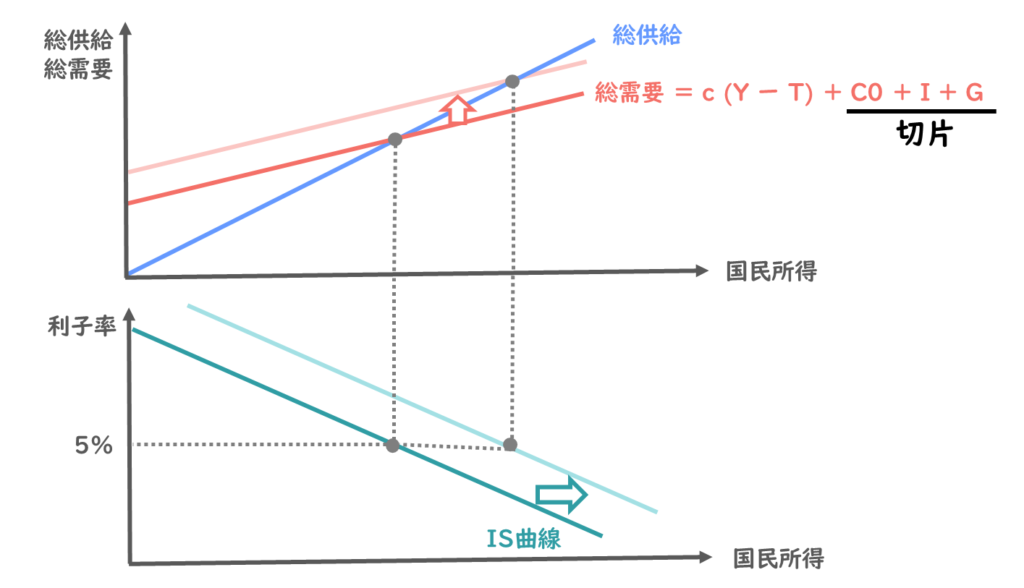
改めてまとめてみると、政府支出が増えると国民所得が増えます。
この時、利子率は変わらないので、IS曲線は全体として右方向にシフトするということになるわけですね。
反対に政府支出が減少すると、左方向にシフトします。
ここでは例として政府支出を取り上げましたが、独立消費C₀や税金Tに関しても総需要曲線の切片となりますので、これらの値が変わってもIS曲線はシフトすることになります。
切片の値が変わっても利子率は変わらない、というところがポイントとなりますので、こちらもぜひご自身でグラフを描きながら理解を深めていただければと思います。
限界消費性向とIS曲線の関係
続いて、限界消費性向とIS曲線の関係について説明します。
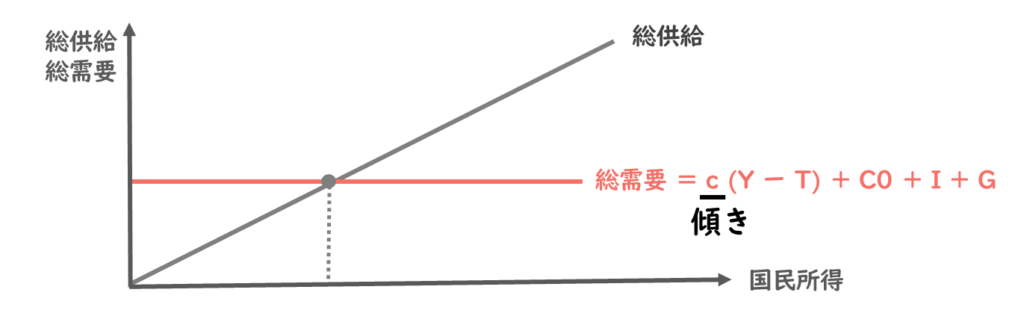
また総需要曲線と総供給曲線を描いてみましょう。
傾きについて確認するときは、総需要曲線はあえて水平方向に描いた方が理解がしやすいかと思います。
限界消費性向は計算式の中ではcで表され、これが総需要曲線の傾きを表すのでしたね。
今、総需要曲線は水平方向となっていますので、限界消費性向は0ということになります。
通常ではありえないケースを確認していることになりますが、あくまで理解を助けるためですので、ご了承ください。
今、利子率が5%から4%に減少して、総需要曲線が上方向にシフトしたことを考えています。
そうするとIS曲線は以下のような直線で表すことができますね。
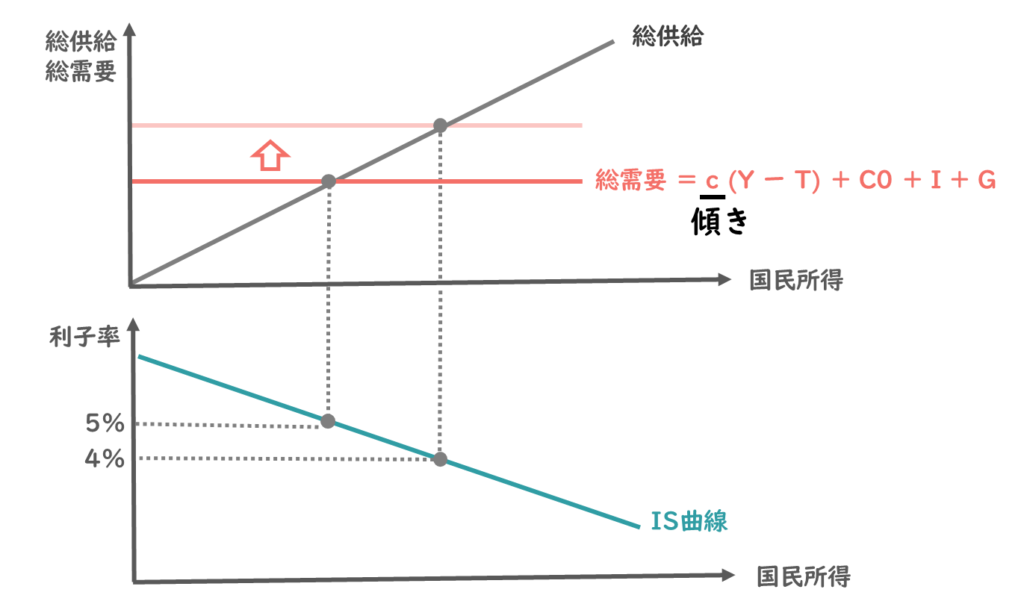
ここで今度は、利子率5%のときの国民所得が全く同じで、総需要曲線の傾きが異なる青の直線を描いてみます。
仮に総需要曲線’(ダッシュ)と置いてみましょう。
この総需要曲線’も同じように、利子率が1%減り、先ほどと同じだけ投資が増えたと考えてみます。
そうすると、同じ分だけ総需要曲線を上方向にシフトさせると、均衡国民所得は以下の位置となりますね。
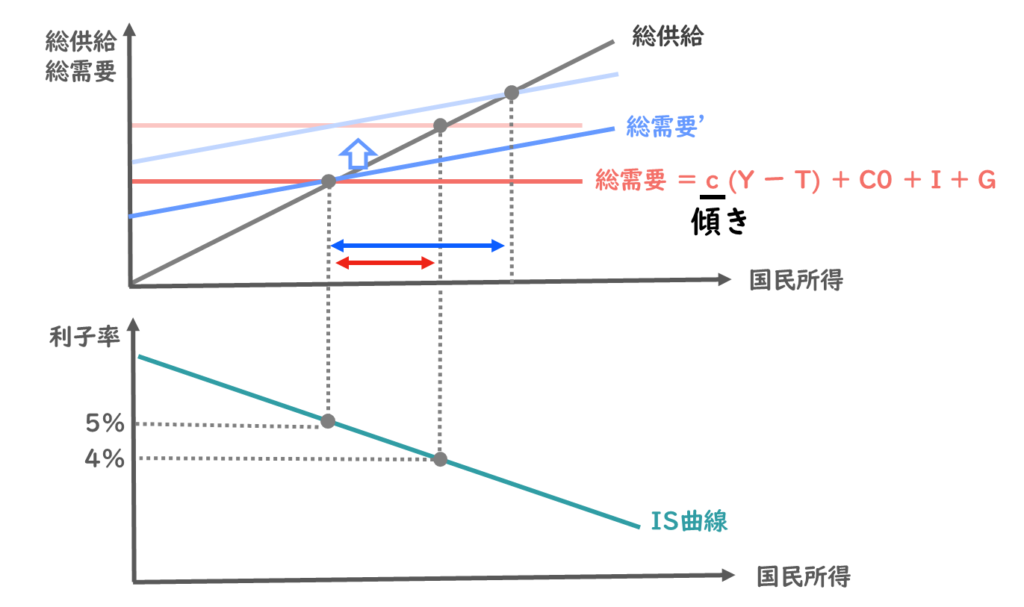
先ほどと比べて、総需要曲線’の国民所得の増加量が大きいことがわかります。
上下のグラフで均衡国民所得は一致しますので、利子率4%のときの国民所得は、今度は以下の位置になりますね。
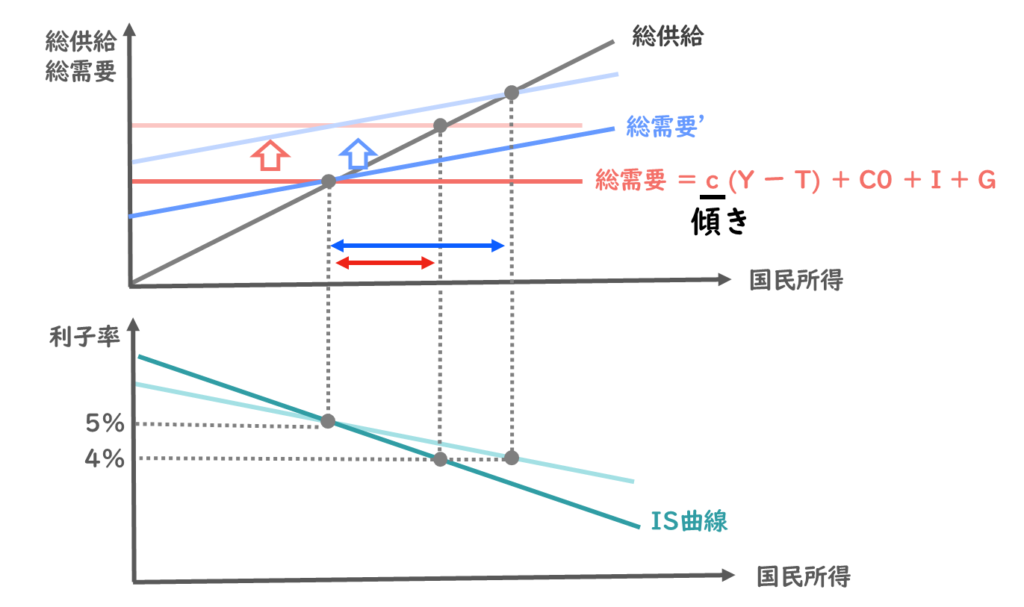
2つの点を結ぶと、新しいIS曲線は上図の薄緑の直線で表すことができますね。
IS曲線の傾きが緩やかになったことが読み取れます。
ここまでの内容をまとめると、限界消費性向が大きくなると、総需要曲線の傾きが大きくなります。
そして利子率の減少量が同じでも国民所得の増加量が増えるため、IS曲線の傾きは緩やかになるということになります。
結論として、限界消費性向が増えると、IS曲線の傾きは緩やかになるということが言えるわけですね。
グラフの中に直線が複数出てきてわかりにくい部分はあったかと思いますが、こちらも重要な考え方の一つですので、ぜひ動画を見返して理解に励んでいただければと思います。
投資の利子率弾力性とIS曲線の関係
最後に、投資の利子率弾力性とIS曲線の関係についても確認します。
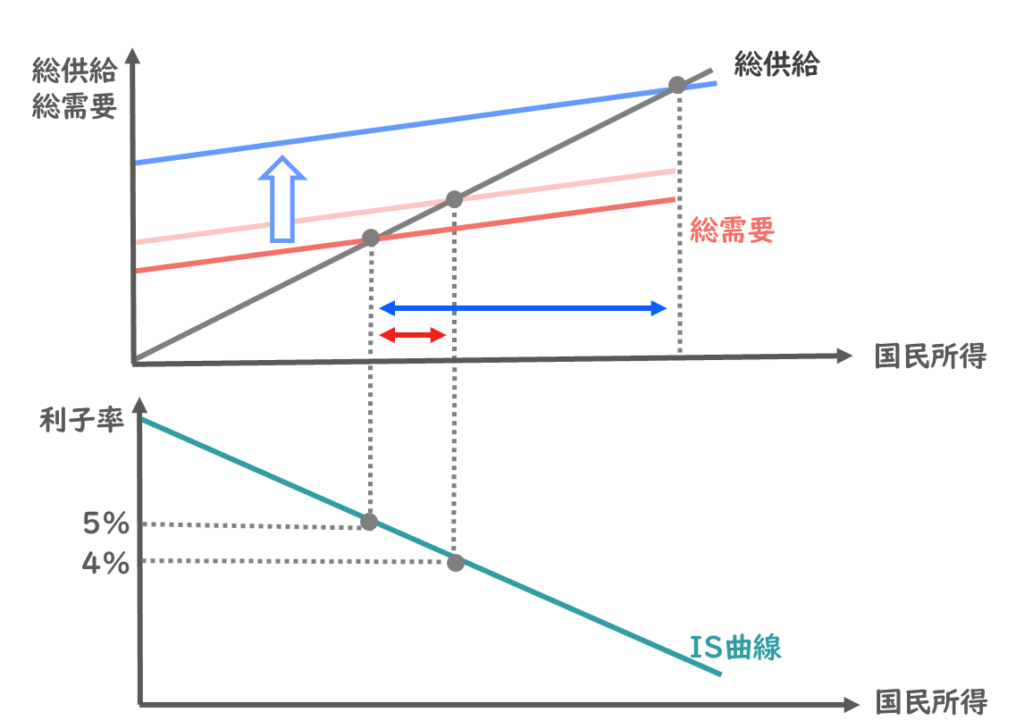
投資の利子率弾力性とは、利子率の変化に対する投資の変化量のことをいいます。
例えば、投資の利子率弾力性が大きい場合、利子率が少ししか変化していないのに、投資は大きく増えるというわけですね。
利子率が5%から4%に減少させたときに、国民所得が増えたとしたら、IS曲線は以下のように描くことができるのでした。
投資の利子率弾力性が大きいということは、同じ1%の減少に対して投資が大きく増えるということを表すのでした。
ですので、投資の利子率弾力性が大きい時は、同じ利子率1%の減少に対しても投資は大きく増加して、総需要曲線は以下の位置くらいまで大きくシフトしたとしましょう。
すると、同じ利子率4%なのに、国民所得は以下の位置にまで増加することになりますので、この2つの直線を結ぶとIS曲線はかなり緩やかな直線になることが読み取れますね。
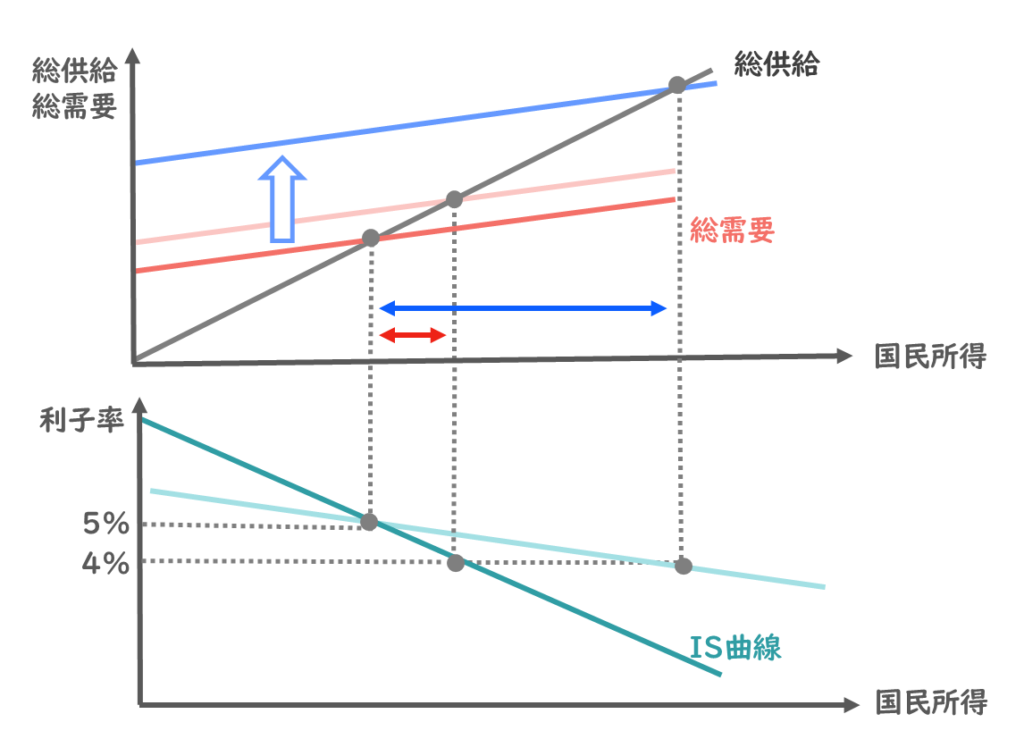
ここまでの内容をまとめると、投資の利子率弾力性が大きいと、利子率の減少量が同じでも投資は大きく増えるということになります。
投資が大きく増えると、国民所得もそれだけ大きく増えることになりますので、IS曲線の傾きは緩やかになるということになるわけですね。
つまり、投資の利子率弾力性が大きいと、IS曲線の傾きは緩やかになります。
投資の利子率弾力性とは何かということを押さえた上で、先ほどの限界消費性向の変化と同じように、IS曲線がどのように変わるのかということをグラフを描きながら確認できるようになれば、この法則も理解できるかと思います。
この辺は理解できるようになるまで少し時間がかかるかと思いますが、繰り返し記事をご覧いただいてマスターいただければと思います。
過去問を解いてみよう (平成21年度 第8問 設問1)
それではここまでの内容を、過去問を解いて復習してみましょう。
IS曲線の特徴に関する説明として、最も適切なものの組み合わせを下記の解答群から選べ。
a IS曲線より右側の領域では、生産物市場は超過供給の状態にある。
b 限界貯蓄性向が大きいほど、IS曲線はより緩やかな形状で描かれる。
c 政府支出の拡大と増税が同じ規模で実施された場合、IS曲線の位置は変わらない。
d 投資の利子感応度が小さいほど、IS曲線はより急な形状で描かれる。
[解答群]
ア aとb イ aとc ウ aとd エ bとc オ cとd
IS曲線の特徴に関するものを選択する問題ですね。
選択肢を一つずつ見ていきましょう。
✅選択肢a
これは今回解説した内容に含まれていない記述ですので、保留とした選択肢となりますね。
✅選択肢b
限界貯蓄性向が大きいということは、限界消費性向が小さいということになります。
限界消費性向が小さければ、IS曲線の傾きはより急な傾きとなりますので、この選択肢は誤りとなりますね。
そもそも限界貯蓄性向と限界消費性向の違いがわからないという方は、総需要曲線のあたりの論点をもう一度復習していただければと思います。
✅選択肢c
政府支出の拡大と増税が同じ規模で実施されるということは、均衡予算を編成したということになりますね。
この時、均衡予算乗数の定理から、国民所得は増税した分だけ増加するのでしたね。
つまり、総需要曲線の切片の値が増えるということになりますので、総需要曲線が上方向にシフトすることになります。
総需要曲線が上方向にシフトすれば、おのずとIS曲線も右方向にシフトすることになりますので、この選択肢も誤りとなりますね。
乗数理論については記事の動画で解説していますので、不安な方は以下から確認してみてください。

✅選択肢d
利子感応度とは、弾力性と意味は同じです。
ですので、「投資の利子率弾力性が小さいと、IS曲線はより急な形状で描かれる」というのは正しい記述ですね。
以上から、保留としていた選択肢aと、選択肢dが正しいという記述となりますので、選択肢ウが正解となります。
選択肢aに関しても、テキストによっては解説があるかと思いますが、やや理解が難しい内容ですので、この問題は消去法的に正解が導き出せれば十分な内容かと思います。
このように、限界消費性向や政府支出、投資の利子率弾力性の変化に対応したIS曲線の変化は頻出論点ですので、ぜひ正解できるよう訓練いただければと思います。
まとめ
それでは最後にまとめです。
今回はIS曲線に関して学習をしました。
IS曲線とは、国民所得と利子率の関係を表す曲線で、横軸に国民所得、縦軸に利子率をとると、このような右肩下がりの曲線として表すことができました。

そして、各種条件に対してIS曲線の変化の仕方は変わるのでした。
政府支出が増加すれば、IS曲線は右方向にシフト、限界消費性向が大きければ傾きが緩やか、投資の利子率弾力性が大きくても傾きは緩やかになるのでした。
この辺はなぜそうなるのかということを、ご自身でグラフを描きながら説明できることが理想的です。
そうすることで丸暗記に頼らず、どのような応用論点が来ても対応できるようになるかと思います。
はい、というわけで、今回はIS曲線について解説してみました。
マクロ経済は特に理解の積み上げが重要です。
この後に続くLM曲線やIS-LM分析についても、今回までの内容がわかっていることが前提になりますので、過去の記事も含めて繰り返しご覧いただいて、理解を深めておいていただければと思います。






























