はいどうも、中小企業診断士のたかぴーです。
今回はIS-LM分析をテーマに解説していきたいと思います。
これまでIS曲線・LM曲線を個別に解説してきましたが、今回はいよいよ2つの曲線を合わせて経済政策を分析する手法を解説します。
いつも通りグラフを用いながら丁寧に解説したいと思いますので、ぜひ最後までご覧ください。
財市場と貨幣市場
前回までで財市場と貨幣市場を学習しました。
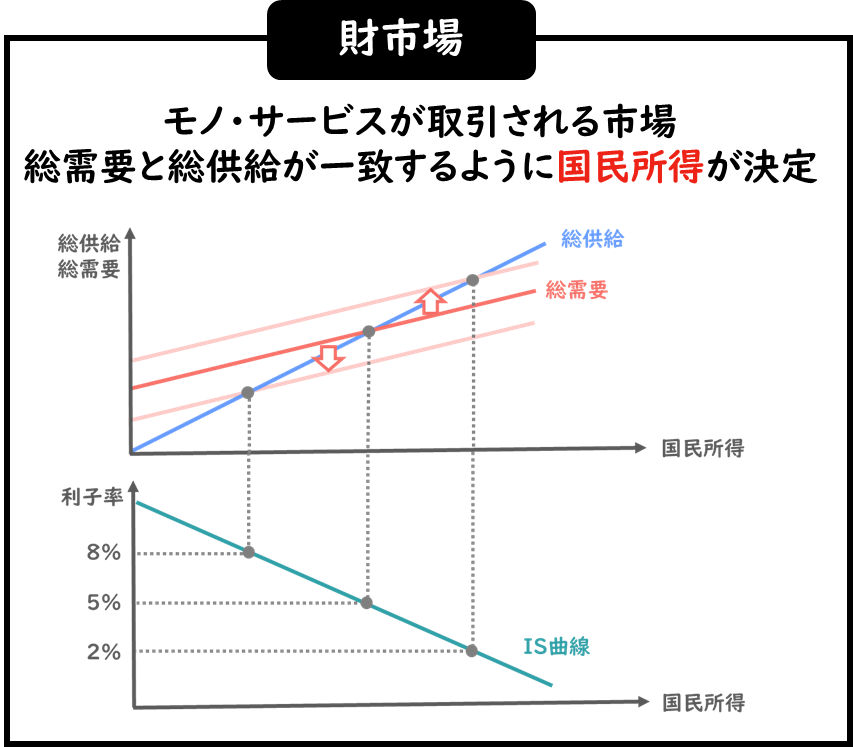
財市場は、サービスが取引される市場のことで、総需要と総供給が一致するように国民所得が決定し、IS曲線は右肩下がりの直線として表されるのでしたね。
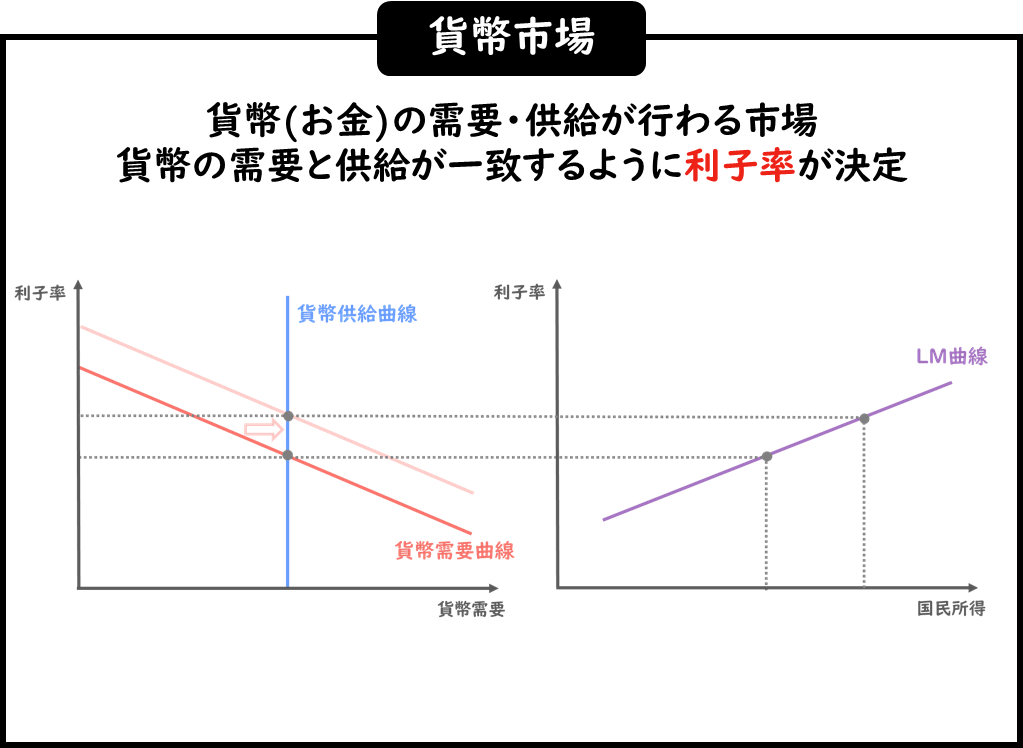
一方、貨幣市場は貨幣の需要と供給が行われる市場のことで、貨幣の需要と供給が一致するように利子率が決まり、LM曲線は右肩上がりの直線として表すことができるのでした。
今回はこれらのIS-LM曲線の導出過程はバッチリ理解できている前提で解説していきますので、この辺に自信がないという方は、過去の記事で復習してから戻ってきていただければと思います。


IS-LM分析とは?
それでは本題のIS-LM分析です。
IS-LM分析とは、財市場と貨幣市場が均衡する際の国民所得と利子率の関係から、財政政策や金融政策の効果を分析する手法のことをいいます。
横軸に国民所得、縦軸に利子率を取ると、IS曲線とLM曲線はそれぞれ以下のように描けますね。

2つの線が交差する点の国民所得を均衡国民所得と呼び、利子率は均衡利子率と呼びます。
IS-LM分析では、この均衡国民所得・均衡利子率がどのように変化するかを分析します。
具体的にはIS曲線・LM曲線がシフトした際や、傾きが変わった際に、財政政策や金融政策が、国民所得と利子率にどのような影響を与えるのかを分析するわけですね。
ここからは具体的にグラフを用いながらその内容を確認していきたいと思います。
IS曲線がシフトする場合
まずはIS曲線がシフトする場合です。
政府支出の増加や減税を行うと、国民所得と利子率がともに増加します。
ちなみに、政府支出の増加や減税は、拡張的な財政政策と言います。
それではグラフを用いて内容を確認してみましょう。
今、IS曲線とLM曲線が以下のように描けていたとしましょう。

拡張的な財政政策を行うと、IS曲線は右方向にシフトするのでしたね。
そうすると、利子率3%・国民所得3兆円だった交点が、利子率4%・国民所得4兆円に移動していることが読み取れます。
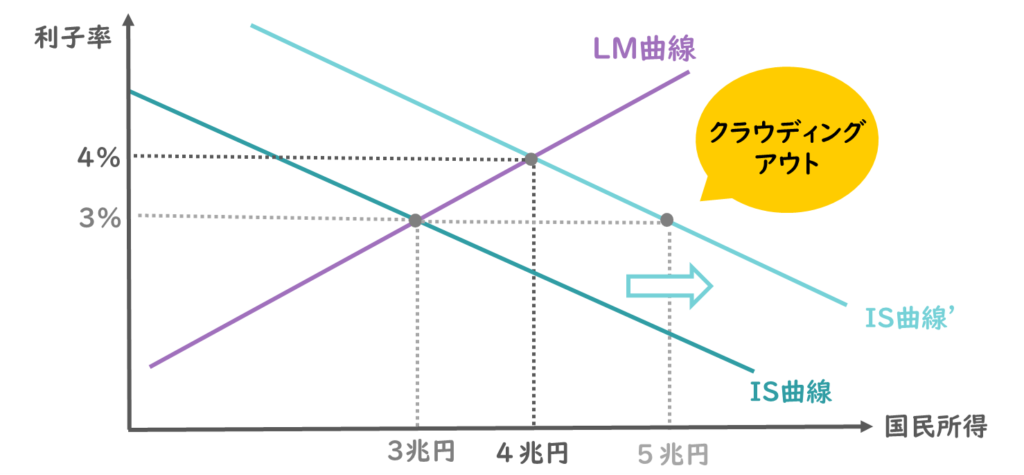
IS-LM分析では、このように財政政策や金融政策を行った際に、IS曲線・LM曲線がどのように変化し、結果として、国民所得や利子率がどのように変化するのかを分析するわけですね。
今回で言うと、拡張的な財政政策が、利子率の増加と引き換えに、国民所得の増加効果があることがわかりました。
ちなみに、IS曲線だけに着目してみると、IS曲線が右方向にシフトすると、同じ利子率3%であれば、国民所得は5兆円にまで増加することが読み取れます。
ですが実際は、均衡国民所得はIS曲線とLM曲線の交点で決まるので、利子率は4%に増加し、その分民間投資が抑えられ、国民所得は5兆円ではなく4兆円にまでしか増えないと考えられます。
このように政府支出を増加した結果、利子率が増加し、結果的に国民所得の増加が抑えられることを「クラウディングアウト」と呼びます。
クラウディングアウトの定義は「拡張的な財政政策が利子率の増加を招くこと」です。
この用語は本試験でもよく出題されますので、内容も併せて覚えておくようにしましょう。
LM曲線がシフトする場合
続いてLM曲線がシフトする場合です。
貨幣供給量を増やすと利子率が下がり、国民所得は増加します。
ちなみに、貨幣供給量を増やすような政策は、金融政策と呼びます。
こちらもグラフを描いて確認してみましょう。
今、均衡国民所得が3兆円、均衡利子率が3%だったとします。

この状態で貨幣供給量を増やして、LM曲線が右方向にシフトしたとすると、均衡国民所得は4兆円・均衡利子率は2%になりましたね。
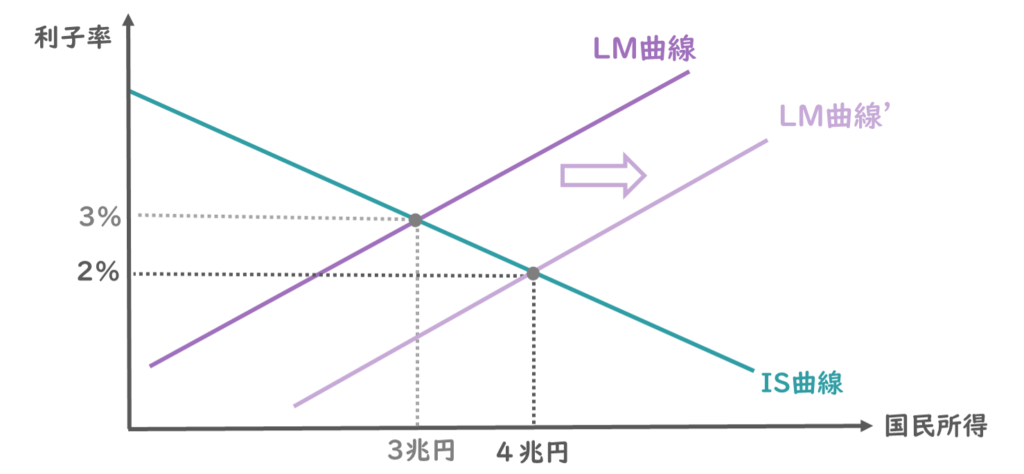
グラフから読み取れる通り、貨幣供給量が増えてLM曲線が右方向にシフトすると、利子率が下がり国民所得が増加するということがわかります。
単純にグラフを読み取るだけで良いので、IS曲線・LM曲線の内容がわかっている方にとっては、そこまで難しい内容ではなかったかと思います。
IS曲線の傾きが変わる場合
続いて、IS曲線の傾きが変わる場合について確認してみましょう。
IS曲線の傾きが緩やかだと、金融政策の効果は大きくなります。
例えば今、IS曲線・LM曲線が以下のように描けていたとしましょう。

この状態で金融政策により貨幣供給量を増やし、LM曲線が右方向にシフトすると、国民所得は4兆円にまで増加することが読み取れますね。

ここまでは先ほど確認した内容と同じです。
今度はIS曲線の傾きが緩やかになる場合を確認したいので、このようにIS曲線が水平であったことを仮定してみましょう。
このように傾きが緩やかか、急かという問題の確認に関しては、水平や垂直な直線を引いて比較すると考えやすくなります。
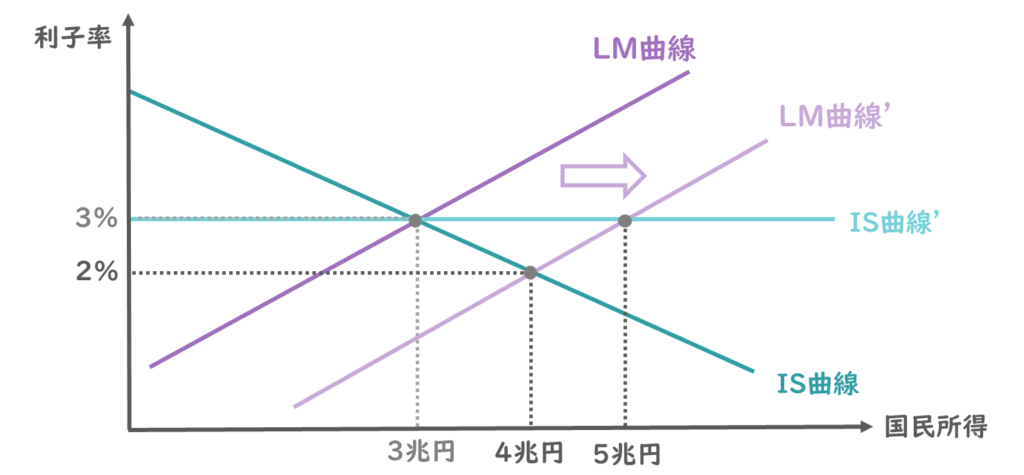
IS曲線が極端に緩やかで水平な場合は、シフト後のLM曲線との交点は、5兆円にまで増加していることが読み取れますね。
つまり、IS曲線の傾きが急な場合と緩やかな場合で比べると、同じLM曲線のシフトに対して国民所得は4兆円から5兆円に大きく増加することになりますので、金融政策の効果は大きくなると言えるわけですね。
LM曲線・IS曲線ともに2本ずつ描いて確認する必要があるので複雑に見えますが、一つ一つ順を追って確認すれば、そう難しいものでもありませんね。
LM曲線の傾きが変わる場合
続いてLM曲線の傾きが変わる場合です。
LM曲線の傾きが緩やかだと、財政政策の効果は大きくなります。
先ほどまでと同じようにグラフで描いて確認してみると、今、均衡国民所得は3兆円、均衡利子率は3%となっていますね。
この状態で政府支出を増やし、IS曲線を右方向にシフトさせると、新しい均衡点は国民所得4兆円、利子率4%に変化していることが読み取れます。

ここまでは先ほど解説した内容ですね。
ここでLM曲線が極端に緩やかで、水平方向であったことを仮定しましょう。
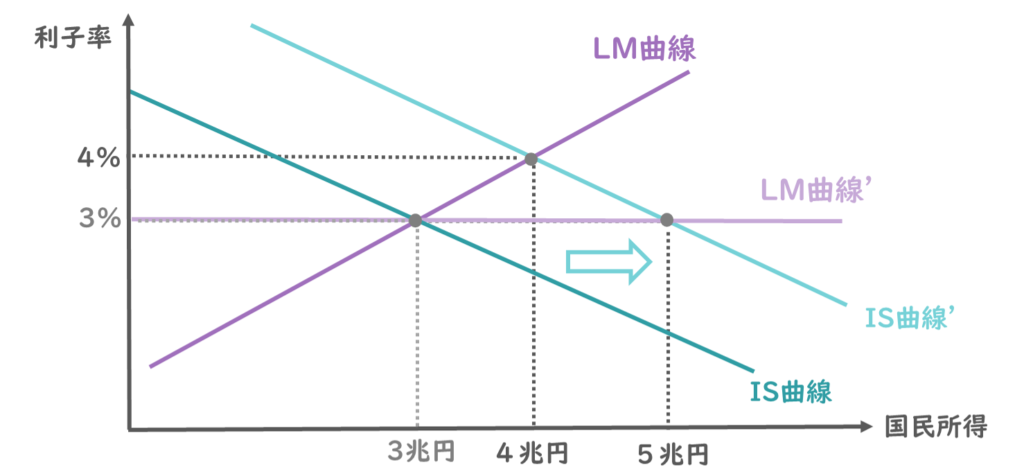
そうするとIS曲線のシフト後の交点は5兆円にまで増加していることが読み取れますね。
つまり、IS曲線の傾き・LM曲線の傾きが緩やかだと、財政政策の効果は大きくなるということが言えるわけです。
ちなみに、LM曲線が緩やかだと利子率は全く変わりませんので、このようにLM曲線が極端に緩やかで水平方向である場合は、IS曲線がシフトしても利子率は全く変わりません。
したがって、先ほど解説したクラウディングアウトが発生しないということになります。
この点も試験に問われることがありますので、考え方を理解しておくようにしましょう。
流動性の罠とは?
最後に流動性の罠です。
流動性の罠とは、利子率が下がっても貨幣需要が極端に高いため、金融政策が効かなくなる状態のことをいいます。
言葉だけだと何を言っているのかわからないと思いますので、こちらもグラフで確認してみましょう。
前回のLM曲線の記事で解説した通り、横軸に貨幣需要、縦軸に利子率を取ると、貨幣需要曲線はこのように右肩下がりの直線として表すことができるのでした。
これは債券の利子率が下がれば下がるほど、債券よりも現金の魅力が相対的に上がるので、貨幣需要がどんどん増えていくことを表しているのでした。
ここで債券の利子率が0.001%という極めて小さな値であるケースを考えてみましょう。
こうなると、仮に債券に100万円投資したとしても年間で1円しか利息はもらえないので、
多くの人は債券なんて買う意味がないので、資産は全て現金で持とうと考えそうです。
つまり、利子率が0.001%よりも小さい値である場合は、貨幣需要は最大、つまり無限大となるので、貨幣需要曲線は以下のように水平方向に描くことができます。
つまり、利子率がこれ以上下がっても、貨幣の需要量は変わらないというわけです。
このように貨幣需要が無限大になり、需要曲線が水平方向で描かれている状態を、「流動性の罠」というわけですね。
流動性の罠が発生しているとき、LM曲線も以下のように水平方向で描くことができます。
そして、利子率が一定水準を超えれば、LM曲線は右肩上がりになるというわけですね。
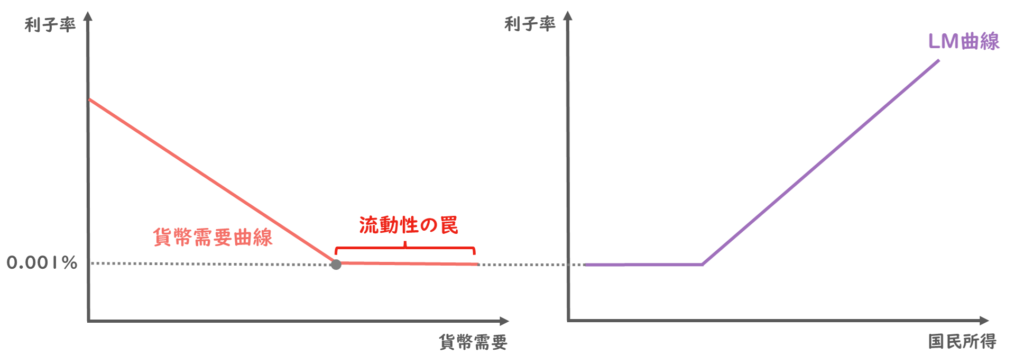
理屈は以上の通りですが、ここは難しいことを考えるより、流動性の罠が発生しているときはLM曲線が水平方向に描かれるという結論だけを覚えていただければ十分かと思います。
なお、今回は利子率0.001%で流動性の罠が発生するとして解説しましたが、これはあくまで例なので、その点はご注意ください。
流動性の罠が発生している場合
それでは流動性の罠が発生している場合のIS-LM分析を行ってみましょう。
流動性の罠が発生している場合、クラウディングアウトは起こらず、金融政策の効果はなくなります。
例えば、流動性の罠が発生している範囲で、IS曲線とLM曲線が交差しているとしましょう。
国民所得は3兆円、利子率は0.001%だとします。
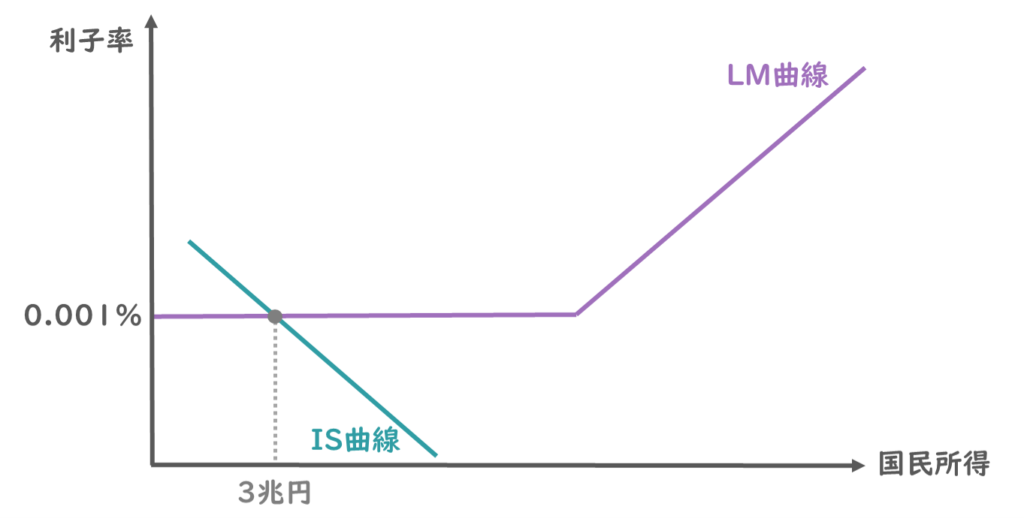
このとき政府支出が増加して、IS曲線が右方向にシフトしたとすると、国民所得は5兆円にまで増加しましたが、利子率は0.001%のまま変わりません。
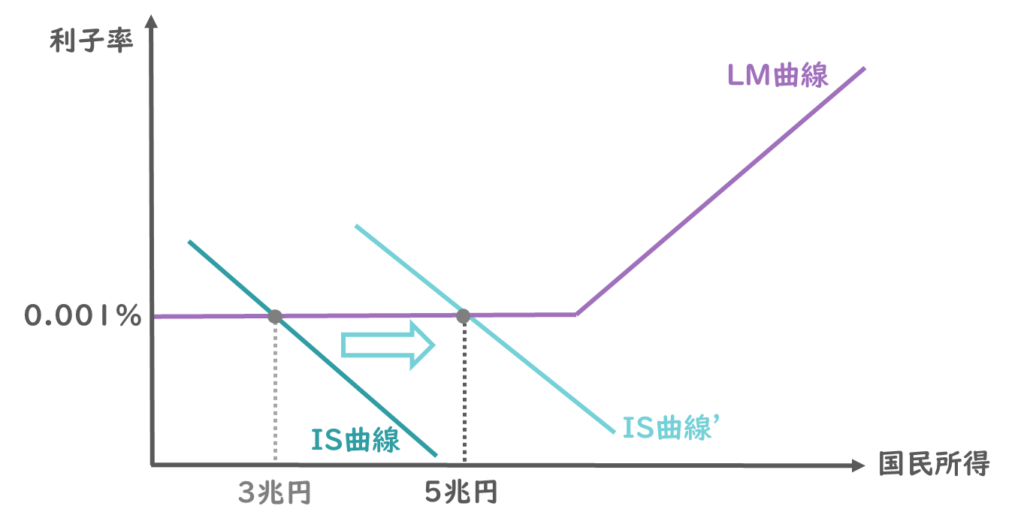
利子率は上がらないので、クラウディングアウトは発生しないということが読み取れますね。
また、貨幣供給量を増やす金融政策を行った場合、LM曲線は右方向にシフトします。
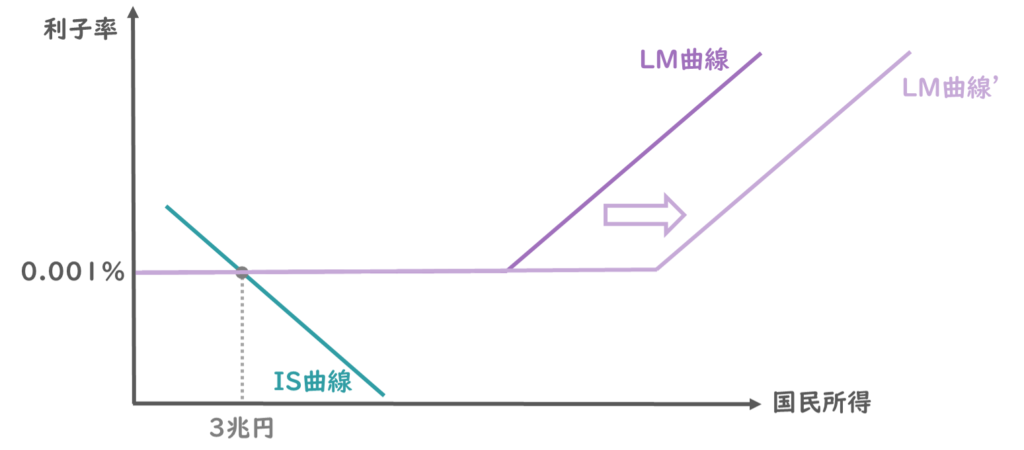
このとき流動性の罠が発生しているのであれば、IS曲線との交点は全く変わりませんので、国民所得の増加効果はないということが読み取れますね。
このように、流動性の罠が発生しているときは、LM曲線が水平であるということだけ理解しておけば、あとはグラフから読み取るだけで大丈夫ですので、こちらもそこまで難しいものではありませんね。
以上、ここまで見てきた通り、IS-LM分析は財政政策や金融政策を行った場合、それぞれのグラフにどのような影響があり、その結果として国民所得や利子率が上がるのか、下がるのかといったことを読み取る必要があります。
逆に言うと、グラフがどのように動き、グラフからどのようなことが読み取れるのかさえ理解できていれば、そんなに難しいものでもありません。
ここは理解が重要となる論点ですので、わからない部分があれば、過去の記事に戻りながら復習していただければと思います。
過去問を解いてみよう(平成26年度 第5問)
それではここまでの内容を、過去問を解いて復習してみましょう。
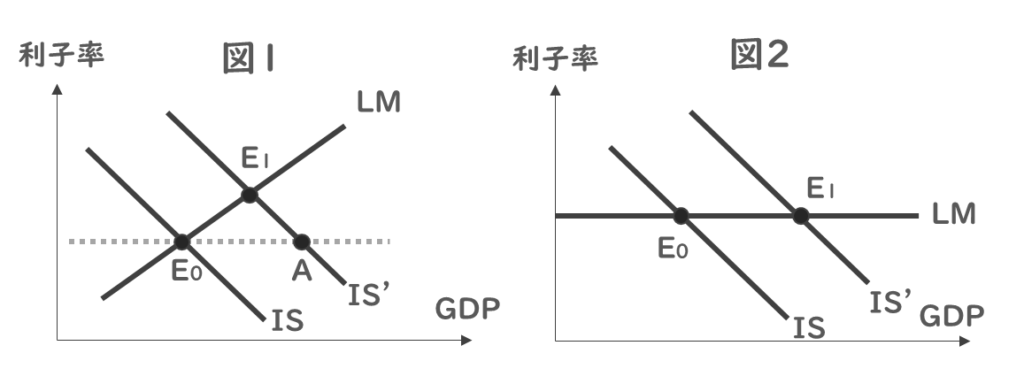
以下の2つの図は、標準的なIS‐LM分析の図である。両図において、初期状態がISとLMの交点であるE0として与えられている。政府支出の増加によってISがIS′に変化したとき、以下の両図に関する説明として最も適切なものを下記の解答群から選べ。
ア 図1が示すところによれば、政府支出の増加による総需要刺激効果は、クラウディング・アウトによって完全に相殺されている。
イ 図1で点Aから点E1までの動きは、「流動性の罠」と呼ばれる状況が生じていることを示している。
ウ 図1で点E0から点Aまでの動きは、政府支出の増加によるクラウディング・アウトの効果を示している。
エ 図2では、政府支出の増加によって利子率が上昇することを示している。
オ 図2では、政府支出の増加によるクラウディング・アウトは発生していない。
IS-LM分析に関する問題ですね。
選択肢を一つ一つ見ていきましょう。
✅選択肢ア
IS曲線が右方向にシフトしたことで、均衡点はE0からE1へと変化していますね。
IS曲線だけに着目すると、国民所得は本来Aまで増加するはずでしたが、利子率が上昇したことでE1に引き戻されています。
ですので、確かにクラウディングアウトが発生してはいますが、国民所得はE0からE1に増加していますので、「完全に相殺されている」という記述は誤りとなります。
したがって、選択肢アは誤りです。
✅選択肢イ
この動きはクラウディングアウトと言うのでしたね。
選択肢イも誤りとなります。
✅選択肢ウ
E0からAまでは、あくまでIS曲線上の変化で、政府支出増加による純粋な需要拡大効果を表しています。
そしてクラウディングアウトは、AからE1への調整で示されるものでした。
したがって、選択肢ウも誤りです。
✅選択肢エ
図から読み取れる通り、IS曲線のシフトによって利子率は上昇しています。
したがって、利子率が変化しないという選択肢エは誤りですね。
✅選択肢オ
「政府支出の増加によるクラウディングアウトは発生していない」とあります。
確かにIS曲線が右にシフトしても、LM曲線が水平であるため、利子率が上がらず、国民所得がその分だけ増加しています。
利子率上昇を伴うクラウディングアウトは発生していませんので、選択肢オは正しい記述ですね。
というわけで、今回の問題は選択肢オが正解です。
用語の意味をしっかり理解して、グラフの動きが読み取れるようになれば、比較的簡単に答えを導ける問題でしたね。
このくらいの難易度であれば確実に正答しておきたいところですので、自信のない方は復習を徹底しておきましょう。
まとめ
今回はIS-LM分析について学習しました。
IS-LM分析とは、財市場と貨幣市場が均衡するときの国民所得と利子率の関係を用いて、
財政政策や金融政策の効果を分析する手法のことでしたね。
具体的には、横軸に国民所得、縦軸に利子率をとり、IS曲線とLM曲線を描くことで、均衡点を求めることができます。

これまでの記事でも解説してきた通り、IS曲線やLM曲線は、政府支出の増減や貨幣供給の変化、限界消費性向や利子率弾力性などの要因によってシフトしたり、傾きが変わったりするのでした。
そして、シフト・傾きに応じて各政策の効果が大きくなるか、小さくなるのかといった点が、試験でよく問われるわけですね。
この内容は、表を丸暗記するのではなく、各政策が実施されたときにグラフがどう動くのか、そして、それによって国民所得や利子率がどう変化するのかを、自分でグラフを描きながら確認できるようになることが重要です。
考え方をしっかり理解すれば、応用問題にも対応できるようになりますので、ぜひこの機会に理解を深めておきましょう。
過去の動画も合わせて基本的な考え方はすべて解説していますので、
過去問演習と記事の復習を繰り返しながら、実力を養っていってください。
はい、というわけで、今回はIS-LM分析について解説してきました。
この論点が理解できるようになると、政府や日銀が行う政策の意図が読み取れるようになります。
ニュースで取り上げられる景気対策や金融政策についても、背景が理解できて、より面白く感じられるようになりますね。
ぜひ皆さんも、この論点をマスターして、経済学の面白さを体感していただければと思います。